La Transformada de Laplace: Descubre cómo calcularla y aplicarla en ecuaciones diferenciales

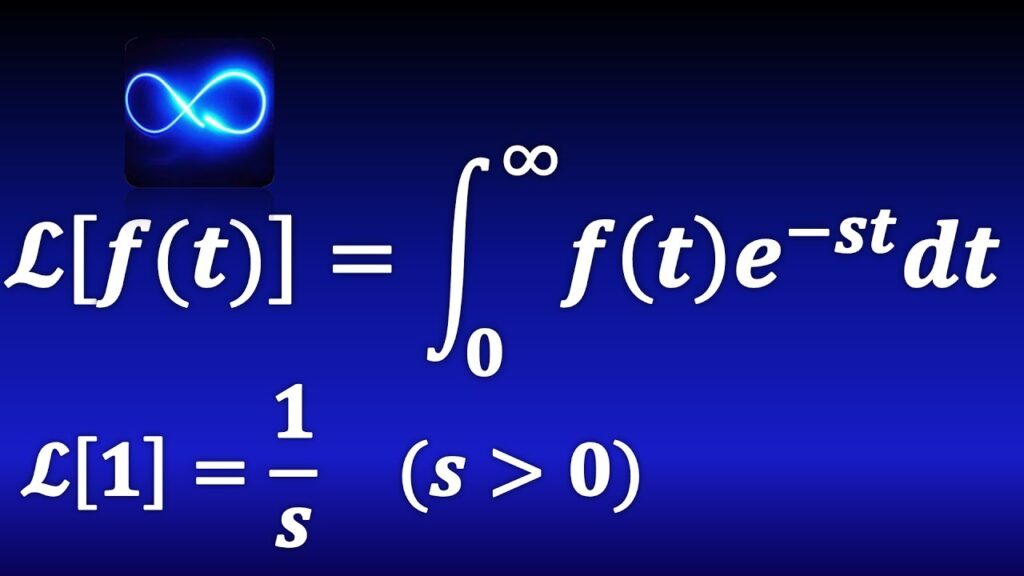
La Transformada de Laplace es una herramienta matemática muy poderosa que se utiliza para resolver ecuaciones diferenciales lineales. Fue desarrollada por el matemático Pierre-Simon Laplace en el siglo I y ha demostrado ser muy útil en diversos campos como la física, la ingeniería y la economía. La transformada de Laplace permite transformar una función en el dominio del tiempo a su correspondiente función en el dominio de la frecuencia.

Exploraremos cómo calcular la transformada de Laplace utilizando la definición integral y las propiedades fundamentales de la transformada. También veremos cómo aplicar esta herramienta a la resolución de ecuaciones diferenciales lineales. Además, daremos algunos ejemplos prácticos para ayudarte a entender cómo funciona la transformada de Laplace y cómo utilizarla en problemas reales. ¡Prepárate para descubrir una forma eficiente de resolver ecuaciones diferenciales!

Qué es la Transformada de Laplace y cómo se calcula

La Transformada de Laplace es una herramienta matemática muy utilizada en el campo de las ecuaciones diferenciales. Fue desarrollada por Pierre-Simon Laplace en el siglo VIII y ha demostrado ser extremadamente útil en la resolución de problemas complejos.

En pocas palabras, la Transformada de Laplace permite convertir una función del dominio del tiempo en una función del dominio de la frecuencia compleja. Esto facilita enormemente el análisis y la resolución de ecuaciones diferenciales lineales ordinarias y parciales.

Pero, ¿cómo se calcula la Transformada de Laplace? En su forma más básica, podemos calcularla mediante la siguiente fórmula integral:

F(s) = ∫ e^(-st) f(t) dt

Donde F(s) representa la función transformada de Laplace de la función original f(t), s es una variable compleja conocida como la variable de transformación y t es la variable independiente del tiempo.

La fórmula anterior puede parecer bastante intimidante a primera vista, pero en realidad es bastante sencilla de aplicar en la práctica. Básicamente, necesitamos evaluar la integral definida para diferentes valores de s y encontrar la función transformada correspondiente.

Para hacer esto, debemos tener en cuenta que existen diferentes reglas y propiedades de la Transformada de Laplace que nos facilitan la tarea. Algunas de estas reglas incluyen:

1. Linealidad

La Transformada de Laplace es una operación lineal, lo que significa que es posible aplicarla a una combinación lineal de funciones. Esto se traduce en que podemos sumar y multiplicar constantes a las funciones antes de aplicar la transformada. Por ejemplo:

L{af(t) + bg(t)} = aF(s) + bG(s)

Donde L{} representa la Transformada de Laplace, f(t) y g(t) son funciones originales, a y b son constantes y F(s) y G(s) son las funciones transformadas correspondientes.

2. Derivadas

La Transformada de Laplace también permite calcular la transformada de una derivada de una función original. Esta propiedad es muy útil para resolver ecuaciones diferenciales lineales. La regla de las derivadas se expresa de la siguiente manera:

L{f'(t)} = sF(s) - f(0)

Donde f'(t) es la derivada de la función original f(t), F(s) es su función transformada y f(0) es el valor inicial de la función original.

3. Integración

Del mismo modo, la Transformada de Laplace también permite calcular la transformada de una integral de una función original. Esta propiedad se expresa de la siguiente manera:

L{∫ f(u) du} = 1/s F(s)

Donde ∫ f(u) du es la integral definida de la función original f(t) y F(s) es su función transformada.

Estas son solo algunas de las principales reglas y propiedades de la Transformada de Laplace. Hay muchas más que se utilizan en diferentes contextos y situaciones, en función de los problemas matemáticos que estemos resolviendo.

En cuanto a la aplicación práctica de la Transformada de Laplace, esta es ampliamente utilizada en ingeniería eléctrica, control automático, física e incluso en economía. Su capacidad para resolver ecuaciones diferenciales lineales con condiciones iniciales y/o en régimen transitorio le otorga una gran flexibilidad y versatilidad.

Además de la resolución de problemas matemáticos, la Transformada de Laplace también se utiliza para analizar el comportamiento de sistemas lineales invariantes en el tiempo. Esto nos permite estudiar su estabilidad, respuesta al impulso y frecuencia, entre otras características.

La Transformada de Laplace es una herramienta fundamental en el campo de las ecuaciones diferenciales y tiene una amplia variedad de aplicaciones prácticas. Aunque su cálculo puede resultar un poco intimidante al principio, con práctica y familiaridad, puedes aprovechar todo su potencial en la resolución de problemas complejos.

Cuál es la utilidad de la Transformada de Laplace en las ecuaciones diferenciales

La Transformada de Laplace es una poderosa herramienta matemática que se utiliza para resolver ecuaciones diferenciales de manera más eficiente y efectiva. A través de la aplicación de esta transformada, podemos analizar el comportamiento de sistemas lineales y encontrar soluciones a ecuaciones diferenciales lineales y no lineales.

Una de las principales utilidades de la Transformada de Laplace en las ecuaciones diferenciales es su capacidad para convertir una ecuación diferencial en una ecuación algebraica. Esto simplifica enormemente el proceso de resolución de ecuaciones diferenciales, permitiéndonos utilizar técnicas más simples y conocidas del álgebra lineal.

Cuando aplicamos la Transformada de Laplace a una ecuación diferencial, obtenemos una función algebraica de la variable compleja s. Esta función, denominada función de transferencia, nos permite estudiar el sistema en el dominio de la frecuencia. Esta perspectiva nos proporciona información sobre cómo se comporta el sistema para diferentes frecuencias de entrada, lo que resulta invaluable en el análisis y diseño de sistemas eléctricos, mecánicos, control automático y muchas otras disciplinas.

Además de su utilidad en el análisis de sistemas físicos, la Transformada de Laplace también encuentra aplicaciones en otras áreas de las matemáticas y la ingeniería. Por ejemplo, se utiliza en la teoría de control para diseñar controladores óptimos y estables para sistemas dinámicos. También se aplica en la teoría de circuitos para analizar y diseñar circuitos eléctricos y electrónicos.

La Transformada de Laplace es una herramienta esencial en el estudio de ecuaciones diferenciales. Su capacidad para convertir ecuaciones diferenciales en ecuaciones algebraicas y su utilidad en el análisis de sistemas en el dominio de la frecuencia hacen de esta transformada una herramienta muy poderosa y versátil en diversas ramas de las matemáticas y la ingeniería.

Cómo se utiliza la Transformada de Laplace para resolver ecuaciones diferenciales lineales

La Transformada de Laplace es una herramienta matemática esencial en la resolución de ecuaciones diferenciales lineales. Esta técnica, desarrollada por Pierre-Simon Laplace en el siglo VIII, permite transformar una ecuación diferencial en el dominio del tiempo a una ecuación algebraica en el dominio de la frecuencia.

Para aplicar la Transformada de Laplace, primero debemos definir la función f(t) que deseamos analizar. La función debe ser continua en todo el intervalo de interés y tener un comportamiento acotado. Una vez tenemos definida nuestra función, podemos aplicar la Transformada de Laplace utilizando la siguiente fórmula:

L(F(t)) = F(s) = ∫ e^(-st) f(t) dt

Donde L(F(t)) denota la función transformada de Laplace de f(t), s es un número complejo y la integral se realiza de 0 a infinito. El objetivo de esta transformación es convertir la ecuación diferencial en el dominio del tiempo en una ecuación algebraica en el dominio de la frecuencia.

Una vez obtenida la transformada de Laplace de la función f(t), debemos aplicar las propiedades y teoremas de la transformada para simplificar la ecuación resultante. Algunas de las propiedades más comunes incluyen:

• Linealidad: L(a*f(t) + b*g(t)) = a*F(s) + b*G(s), donde a y b son constantes.
• Dominio del tiempo: L(dt/dt) = s, L(d^2f(t)/dt^2) = s^2*F(s), L(d^nf(t)/dt^n) = s^n*F(s), donde n es un número natural y d representa la derivada.
• Desplazamiento en el dominio del tiempo: L(e^(at)*f(t)) = F(s-a), donde a es una constante.

Estas propiedades nos permiten simplificar la transformada de Laplace y facilitar su posterior resolución. Una vez simplificada la ecuación algebraica resultante, podemos encontrar la función F(s) inversa aplicando la Transformada de Laplace inversa.

La Transformada de Laplace tiene una amplia gama de aplicaciones en ingeniería, física y matemáticas. Se utiliza para resolver ecuaciones diferenciales lineales, estudiar sistemas dinámicos, analizar circuitos eléctricos, entre otros. Su capacidad para transformar problemas complejos en cálculos más simples la convierte en una herramienta indispensable en diferentes campos.

La Transformada de Laplace es una técnica matemática poderosa que permite transformar una ecuación diferencial en el dominio del tiempo en una ecuación algebraica en el dominio de la frecuencia. Su utilización nos brinda la capacidad de resolver ecuaciones diferenciales lineales, analizar sistemas dinámicos y estudiar una amplia variedad de fenómenos físicos y matemáticos. Si deseas adentrarte en el apasionante mundo de las ecuaciones diferenciales, la Transformada de Laplace sin duda será una herramienta imprescindible en tu arsenal.

Cuáles son las propiedades básicas de la Transformada de Laplace

La Transformada de Laplace es una herramienta matemática extremadamente útil en el campo de las ecuaciones diferenciales. Esta transformada nos permite convertir ecuaciones diferenciales en ecuaciones algebraicas, lo que facilita su análisis y resolución. Para comprender mejor esta poderosa herramienta, es fundamental conocer sus propiedades básicas.

1. Linealidad

Una de las propiedades más importantes de la Transformada de Laplace es su linealidad. Esto significa que si tenemos una combinación lineal de funciones (f(t) = a * f1(t) + b * f2(t)), la transformada de Laplace de f(t) será igual a la combinación lineal de las transformadas de Laplace de cada función individual (F(s) = a * F1(s) + b * F2(s)). Esta propiedad es especialmente útil a la hora de resolver ecuaciones diferenciales lineales con condiciones iniciales.

2. Desplazamiento en el eje s

Otra propiedad importante es el desplazamiento en el eje s. Si tenemos una función f(t) y le agregamos una constante c al argumento del tiempo (f(t-c)), entonces la transformada de Laplace de f(t-c) será igual a e^(-cs) multiplicado por la transformada de Laplace de f(t). En otras palabras:

L{f(t-c)} = e^(-cs) * F(s)

Esta propiedad nos permite desplazar en el tiempo una señal y analizar su comportamiento en un instante diferente. Es particularmente útil cuando queremos estudiar sistemas dinámicos que responden a cambios en el tiempo.

3. Derivación en el dominio s

La Transformada de Laplace nos permite derivar funciones en el dominio s mediante una propiedad conocida como derivación en el dominio s. Si tenemos una función f(t) y tomamos su derivada con respecto al tiempo, esto se traduce en la multiplicación por s en el dominio de Laplace. Matemáticamente hablando:

L{f'(t)} = s * F(s) - f(0)

Esta propiedad nos facilita la resolución de ecuaciones diferenciales lineales, ya que podemos tomar la transformada de Laplace de ambas partes de la ecuación y resolverla algebraicamente en el dominio s.

4. Integración en el dominio s

Así como podemos derivar funciones en el dominio s, también podemos realizar la operación inversa: integrar. Cuando tomamos la integral de una función en el dominio temporal, esto se traduce en la división por s en el dominio de Laplace. En términos matemáticos:

L{∫f(t)dt} = F(s) / s

Esta propiedad es especialmente útil cuando queremos resolver ecuaciones diferenciales integrales utilizando la Transformada de Laplace. Nos permite convertir operaciones de integración en cálculos de división simple.

5. Teorema del valor inicial

Otra propiedad importante de la Transformada de Laplace es el teorema del valor inicial. Este teorema establece que si una función f(t) tiene una transformada de Laplace F(s), entonces el valor inicial de f(t) (es decir, f(0)) se puede obtener encontrando el límite de s * F(s) cuando s tiende a infinito. Matemáticamente:

f(0) = lim(s → ∞) of

Esta propiedad nos permite calcular el valor inicial de una función directamente a partir de su transformada de Laplace, evitando la necesidad de realizar cálculos adicionales.

6. Teorema del valor final

Por último, tenemos el teorema del valor final, que establece que si una función f(t) tiene una transformada de Laplace F(s), entonces el valor final de f(t) (es decir, lim(t → ∞) of f(t)) se puede obtener encontrando el límite de s * F(s) cuando s tiende a cero. En términos matemáticos:

lim(t → ∞) of f(t) = lim(s → 0) of

Al igual que el teorema del valor inicial, este teorema nos permite calcular el valor final de una función directamente a partir de su transformada de Laplace, sin necesidad de resolver la ecuación en el dominio temporal.

Estas son solo algunas de las propiedades básicas de la Transformada de Laplace. Sin embargo, son fundamentales para comprender y aplicar adecuadamente esta poderosa herramienta matemática en el análisis y resolución de ecuaciones diferenciales. Conocer estas propiedades nos permite simplificar los cálculos y obtener soluciones más rápidas y precisas.

Cómo se aplica la Transformada de Laplace en problemas de valor inicial

La Transformada de Laplace es una herramienta matemática que resulta muy útil para solucionar ecuaciones diferenciales lineales. En particular, se utiliza con frecuencia en problemas de valor inicial, donde se conoce el valor inicial de la función y se busca determinar cómo evoluciona a lo largo del tiempo.

Para aplicar la Transformada de Laplace en problemas de valor inicial, hay varios pasos clave que debemos seguir:

Paso 1: Definir la función inicial

En primer lugar, debemos definir la función inicial que describe el sistema que queremos estudiar. Esta función debe ser una función temporal y estar definida en el intervalo de tiempo de interés.

Paso 2: Aplicar la Transformada de Laplace

A continuación, aplicamos la Transformada de Laplace a la función inicial. La Transformada de Laplace convierte una función de dominio temporal en una función de dominio complejo, lo que nos permite trabajar con ecuaciones diferenciales en el dominio de la frecuencia.

L(f(t)) = F(s)

Donde L representa la Transformada de Laplace, f(t) es la función inicial y F(s) es la función transformada.

Paso 3: Resolver la ecuación transformada

Una vez que tenemos la función transformada, podemos resolver la ecuación correspondiente al problema de valor inicial en el dominio de la frecuencia. Esto implica algebraicamente manipular la función transformada y aplicar propiedades de la Transformada de Laplace según sea necesario.

Paso 4: Determinar la función en el dominio temporal

Una vez que hemos resuelto la ecuación transformada en el dominio de la frecuencia, podemos aplicar la Transformada inversa de Laplace para volver al dominio temporal y obtener la solución del problema de valor inicial original.

L-1(F(s)) = f(t)

Donde L-1 representa la Transformada inversa de Laplace y f(t) es la función resultante en el dominio temporal.

Para aplicar la Transformada de Laplace en problemas de valor inicial, debemos definir la función inicial, aplicar la Transformada de Laplace, resolver la ecuación transformada y finalmente determinar la función resultante en el dominio temporal utilizando la Transformada inversa de Laplace. Este proceso nos permite analizar y comprender cómo una función evoluciona a lo largo del tiempo, lo que resulta fundamental en áreas como la ingeniería, la física y la economía, entre otras.

Cuál es la relación entre la Transformada de Laplace y los sistemas lineales invariables en el tiempo

La Transformada de Laplace es una poderosa herramienta matemática que se utiliza para resolver ecuaciones diferenciales lineales. Esta transformada convierte una función de dominio temporal en una función de dominio complejo, lo que nos permite analizar su comportamiento en el plano complejo.

Una de las principales aplicaciones de la Transformada de Laplace es en el estudio de los sistemas lineales invariables en el tiempo. Estos sistemas son aquellos cuyas propiedades y comportamiento no cambian con el paso del tiempo. Son ampliamente utilizados en áreas como la ingeniería eléctrica, la mecánica, la física y la economía, entre otras.

La relación entre la Transformada de Laplace y los sistemas lineales invariables en el tiempo se basa en el hecho de que la transformada de una señal de entrada aplicada a un sistema lineal invariable en el tiempo produce la transformada de la respuesta del sistema. En otras palabras, si conocemos la transformada de una señal de entrada y la función de transferencia del sistema, podemos obtener la transformada de la respuesta del sistema.

Cómo calcular la Transformada de Laplace de una función

Existen diversas técnicas y métodos para calcular la Transformada de Laplace de una función. A continuación, presentaremos algunas de las más comunes:

• Método de fracciones parciales: este método se utiliza cuando la función a transformar presenta términos de tipo fraccionario. Consiste en descomponer la función en una suma de fracciones simples y luego aplicar la Transformada de Laplace a cada una de ellas.
• Tabla de transformadas de Laplace: existe una tabla con las transformadas más comunes, que incluye funciones como exponenciales, senos y cosenos, entre otras. Esta tabla es una herramienta útil para calcular la transformada de una función de manera rápida y sencilla.
• Propiedades de la Transformada de Laplace: existen varias propiedades algebraicas que nos permiten simplificar el cálculo de la Transformada de Laplace. Algunas de estas propiedades son la linealidad, la derivación y la integración en el dominio del tiempo.

Cómo aplicar la Transformada de Laplace en ecuaciones diferenciales

La Transformada de Laplace es especialmente útil en la resolución de ecuaciones diferenciales lineales, ya que permite convertir una ecuación diferencial en una ecuación algebraica mucho más fácil de resolver.

Para aplicar la Transformada de Laplace en ecuaciones diferenciales, se deben seguir los siguientes pasos:

1. Aplicar la Transformada de Laplace a ambos lados de la ecuación diferencial.
2. Utilizar las propiedades de la Transformada de Laplace para simplificar la ecuación resultante en una ecuación algebraica.
3. Resolver la ecuación algebraica obtenida, generalmente mediante despeje de la variable desconocida.
4. Finalmente, aplicar la Transformada inversa de Laplace para obtener la solución en el dominio temporal.

Es importante destacar que la Transformada de Laplace no solo nos permite resolver ecuaciones diferenciales lineales, sino que también ofrece una gran ventaja en términos de estabilidad y análisis de sistemas lineales invariables en el tiempo.

La Transformada de Laplace es una herramienta fundamental en el estudio de los sistemas lineales invariables en el tiempo. Su uso nos permite analizar el comportamiento de señales y sistemas en el dominio complejo, facilitando la resolución de ecuaciones diferenciales y proporcionando información relevante sobre la estabilidad y respuesta de los sistemas.

Existen inversiones de la Transformada de Laplace para obtener soluciones en el dominio temporal

La Transformada de Laplace es una herramienta matemática muy útil en el estudio y solución de ecuaciones diferenciales. Una vez que hemos obtenido la función transformada de una ecuación diferencial en el dominio de la frecuencia, nos encontramos ante el desafío de regresar al dominio temporal para obtener la solución deseada.

Afortunadamente, existe un conjunto de técnicas conocidas como inversiones de la Transformada de Laplace que nos permiten obtener la solución en el dominio temporal a partir de la función transformada. Estas técnicas se basan en la utilización de tablas de transformadas inversas y propiedades de la Transformada de Laplace.

Método de las fracciones parciales

• Este método se utiliza cuando la función transformada de Laplace presenta una forma algebraica compleja con polinomios en el denominador.
• Consiste en descomponer la función transformada en fracciones más simples utilizando las raíces del denominador en forma de factores lineales o cuadráticos.
• A través de esta descomposición, obtenemos una suma de términos más sencillos que pueden ser invertidos fácilmente mediante el uso de las propiedades de la Transformada de Laplace.

Método de la expansión en series de Taylor

• Este método se utiliza cuando la función transformada de Laplace no es expresable mediante fracciones parciales.
• Consiste en desarrollar la función transformada en una serie de potencias utilizando la conocida serie de Taylor.
• Este desarrollo nos permite obtener una aproximación de la función transformada mediante una suma infinita de términos polinomiales.
• Posteriormente, utilizando las propiedades de la Transformada de Laplace, podemos invertir cada término de la serie de Taylor para obtener la solución en el dominio temporal.

Otros métodos de inversión

Además de los dos métodos anteriores, existen otros métodos más avanzados para realizar inversiones de la Transformada de Laplace. Algunos de estos métodos incluyen el uso de integrales definidas, series asintóticas y métodos numéricos.

Contar con técnicas de inversión de la Transformada de Laplace es fundamental para poder utilizar esta poderosa herramienta matemática en la solución de ecuaciones diferenciales en el dominio temporal. Los métodos de fracciones parciales, expansión en series de Taylor y otros métodos más avanzados nos permiten obtener la solución deseada a partir de la función transformada. Es importante conocer y dominar estos métodos para poder aplicar correctamente la Transformada de Laplace en problemas reales.

Cuáles son las ventajas de utilizar la Transformada de Laplace en la resolución de ecuaciones diferenciales frente a otros métodos

La Transformada de Laplace es una herramienta matemática muy poderosa que se utiliza para resolver ecuaciones diferenciales lineales. Aunque existen otros métodos para resolver tales ecuaciones, la Transformada de Laplace presenta ciertas ventajas distintivas y puede resultar especialmente útil en determinadas situaciones.

Simplicidad y rapidez en la resolución

Una de las principales ventajas de utilizar la Transformada de Laplace es su simplicidad y rapidez en la resolución de ecuaciones diferenciales. Al aplicar esta transformada, la ecuación diferencial se convierte en una ecuación algebraica más sencilla de resolver. Esto permite simplificar el proceso de solución y agiliza el cálculo.

Generalización de problemas complejos

Otra ventaja destacable de la Transformada de Laplace es su capacidad para generalizar la solución de problemas complejos. Esta transformada puede aplicarse a ecuaciones diferenciales de cualquier orden y con coeficientes variables, lo cual amplía su alcance y ofrece una mayor flexibilidad en la resolución de distintos tipos de problemas.

Aproximación de soluciones en dominio temporal continuo

La Transformada de Laplace permite representar funciones en el dominio temporal continuo mediante funciones racionales en el dominio de la frecuencia compleja. Esto facilita la aproximación y análisis de soluciones en el tiempo, lo que resulta especialmente útil en el estudio de sistemas dinámicos y fenómenos físicos que evolucionan en el tiempo.

Manejo de condiciones iniciales y finales

La Transformada de Laplace también ofrece una forma sencilla y elegante de manejar las condiciones iniciales y finales en problemas de ecuaciones diferenciales. Al aplicar esta transformada, dichas condiciones se incorporan directamente en la función transformada, simplificando el proceso de solución y permitiendo obtener resultados más rápidamente.

Aplicación en sistemas lineales invariantes en el tiempo

La Transformada de Laplace es ampliamente utilizada en el estudio y análisis de sistemas lineales invariantes en el tiempo. Esta herramienta matemática permite analizar la estabilidad, respuesta en frecuencia y comportamiento en el tiempo de estos sistemas, lo cual resulta fundamental en disciplinas como la ingeniería eléctrica, la electrónica y la mecánica.

La Transformada de Laplace presenta numerosas ventajas que la convierten en una herramienta indispensable para la resolución de ecuaciones diferenciales. La simplicidad y rapidez en la resolución, la capacidad de generalización, la aproximación de soluciones en dominio temporal continuo, el manejo de condiciones iniciales y finales, y su aplicación en sistemas lineales invariantes en el tiempo la hacen extremadamente útil en una variedad de disciplinas científicas y tecnológicas.

Cómo se realiza la Transformada de Laplace de funciones periódicas o no periódicas

La Transformada de Laplace es una herramienta matemática que se utiliza para analizar funciones y ecuaciones diferenciales. Es especialmente útil en casos donde no es posible resolver una ecuación diferencial de manera directa, ya sea debido a la complejidad de la función o a la falta de conocimiento sobre las soluciones exactas.

La Transformada de Laplace puede aplicarse tanto a funciones periódicas como no periódicas. En el caso de funciones periódicas, es necesario tener en cuenta que la transformada de una función periódica puede no existir si la integral que define la transformada diverge. Sin embargo, en muchos casos prácticos, es posible obtener una expresión analítica para la transformada de una función periódica haciendo uso de propiedades y resultados previamente establecidos.

Cálculo de la Transformada de Laplace para funciones no periódicas

Para calcular la Transformada de Laplace de una función no periódica, se utiliza la siguiente fórmula integral:

L(f(t)) = F(s) = ∫ e^(-st)f(t) dt

donde L(f(t)) representa la Transformada de Laplace de la función f(t), F(s) es la función obtenida después de realizar la transformada y s es una variable compleja.

La integral se realiza desde 0 hasta infinito, lo cual implica que la función debe ser causal, es decir, que su valor debe ser igual a cero para valores negativos de t. Esto se debe a que la integral considera todas las posibles contribuciones de la función en el tiempo.

Una vez realizada la integral, se obtiene una función de la variable compleja s, que representa la frecuencia compleja. Esta función puede tener diversos usos, como por ejemplo, encontrar soluciones analíticas para ecuaciones diferenciales lineales o evaluar el comportamiento de un sistema en el dominio de la frecuencia.

Cálculo de la Transformada de Laplace para funciones periódicas

En el caso de las funciones periódicas, es necesario hacer uso de conceptos adicionales. La Transformada de Laplace de una función periódica se define utilizando una serie de Fourier:

F(s) = ∑ C(n) /

donde F(s) representa la Transformada de Laplace de la función periódica, C(n) son los coeficientes de la serie de Fourier y ωn son las frecuencias armónicas.

El cálculo de los coeficientes de la serie de Fourier depende de las propiedades de la función periódica en cuestión. Estos coeficientes pueden obtenerse a través de integrales o mediante otras técnicas, como la convolución de funciones.

• Propiedad de dualidad: Si la función f(t) tiene su Transformada de Laplace F(s), entonces la Transformada de Laplace de F(t) será igual a 2πf(-s).
• Propiedad de desplazamiento en el tiempo: La Transformada de Laplace de una función desplazada en el tiempo está relacionada con la Transformada de Laplace sin desplazamiento mediante una exponencial compleja.

Es importante destacar que el cálculo de la Transformada de Laplace de una función periódica puede ser más complejo que en el caso de funciones no periódicas, debido a la necesidad de trabajar con series y coeficientes de Fourier. Sin embargo, esta herramienta resulta invaluable para analizar sistemas eléctricos, mecánicos y otros campos donde las funciones periódicas son comunes.

Puedo utilizar la Transformada de Laplace para resolver cualquier tipo de ecuación diferencial

La Transformada de Laplace es una poderosa herramienta matemática que permite resolver ecuaciones diferenciales de una manera más sencilla y eficiente. Si bien existen varios métodos para resolver ecuaciones diferenciales, la Transformada de Laplace se destaca por su versatilidad y aplicabilidad en diferentes casos.

Uno de los mayores beneficios de utilizar la Transformada de Laplace es que se puede aplicar a cualquier tipo de ecuación diferencial, ya sean lineales o no lineales. Esto nos proporciona una solución generalizada que es válida independientemente de las características específicas de la ecuación.

Además, la Transformada de Laplace nos permite convertir una ecuación diferencial en una ecuación algebraica más manejable. Esto simplifica en gran medida el proceso de resolución, ya que el álgebra es una herramienta ampliamente conocida y utilizada en las matemáticas.

Para utilizar la Transformada de Laplace en una ecuación diferencial, primero debemos aplicar la transformada a ambos lados de la ecuación. Esta transformada convierte un problema de derivadas en un problema de multiplicación y suma de funciones.

Una vez que hemos aplicado la Transformada de Laplace, obtenemos una nueva ecuación algebraica en términos de la variable compleja 's'. Esta ecuación nos proporciona una función de transferencia que relaciona la entrada con la salida del sistema.

La función de transferencia resultante nos permite analizar el comportamiento del sistema ante diferentes señales de entrada, lo que nos da una idea clara de cómo se comportará la respuesta del sistema en el tiempo. Esto es especialmente útil en ingeniería y física, donde necesitamos comprender y predecir el comportamiento de sistemas complejos.

Es importante destacar que la Transformada de Laplace también nos brinda herramientas para analizar la estabilidad y la convergencia de un sistema. A través del análisis de los polos y ceros de la función de transferencia, podemos determinar si el sistema será estable o no, lo que es fundamental en el diseño y control de sistemas.

La Transformada de Laplace es una técnica matemática invaluable para resolver ecuaciones diferenciales de manera eficiente y generalizada. Su aplicabilidad a cualquier tipo de ecuación y su capacidad para simplificar el proceso de resolución la convierten en una herramienta esencial en el campo de las ciencias e ingeniería.

La Transformada de Laplace es una herramienta matemática que permite transformar una función en el dominio del tiempo a una función en el dominio de la frecuencia.

La Transformada de Laplace se utiliza principalmente en el estudio y solución de ecuaciones diferenciales lineales, ya que facilita su resolución al llevar las variables de dominio tiempo a dominio frecuencia.

La Transformada de Laplace se calcula aplicando la fórmula integral de la transformada de Laplace, que consiste en integral la función multiplicada por un factor exponencial negativo de la variable tiempo.

La propiedad de linealidad es fundamental en la Transformada de Laplace, ya que nos permite calcular la transformada de una combinación lineal de funciones sumando las transformadas individuales de cada función.

En la Transformada de Laplace, los polos se corresponden con los valores de las variables para los cuales la función transformada se vuelve infinita, mientras que los ceros son aquellos valores que anulan la función transformada.