El Teorema del Límite Central: La fórmula que revela el secreto detrás de las estadísticas

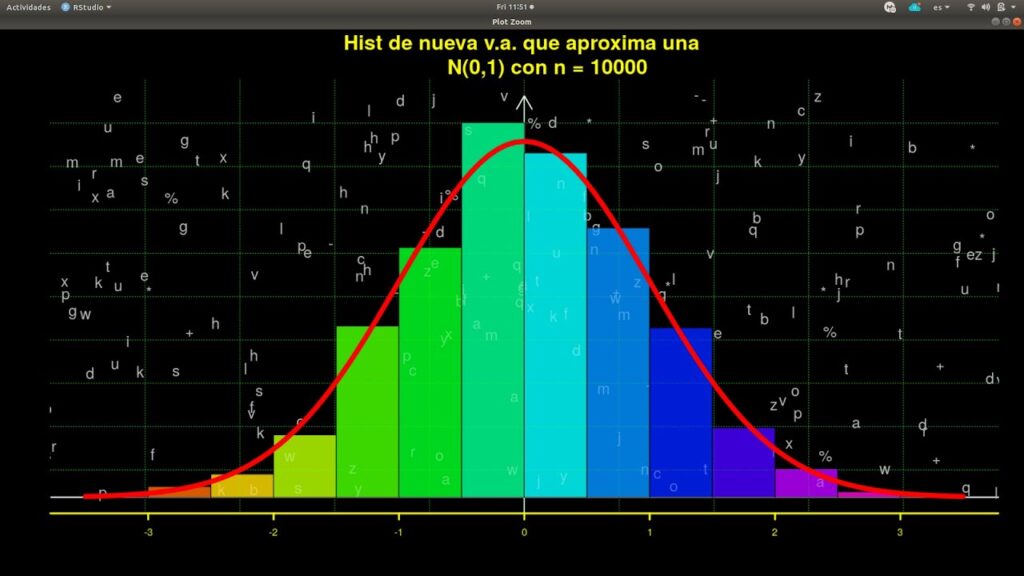
En el campo de la estadística, muchas veces nos enfrentamos a la tarea de analizar grandes cantidades de datos para tomar decisiones informadas. Para hacer esto, es fundamental contar con herramientas y métodos que nos permitan extraer conclusiones válidas a partir de esos datos. Uno de los conceptos más importantes en este sentido es el Teorema del Límite Central.

El Teorema del Límite Central afirma que, cuando se toman muestras aleatorias suficientemente grandes de una población, la distribución de las medias muestrales se aproxima a una distribución normal. Esto significa que, independientemente de la forma en que esté distribuida la población original, al tomar suficientes muestras de tamaño n y calcular sus medias, obtendremos una curva de distribución que sigue una forma de campana característica de la distribución normal.

Qué es el Teorema del Límite Central y por qué es importante en estadísticas

El Teorema del Límite Central (TLC) es uno de los conceptos fundamentales en estadísticas que nos permite comprender mejor la distribución de los datos y cómo se relacionan con la media poblacional. Este teorema establece que, independientemente de la forma de la distribución original, la suma o promedio de un gran número de variables aleatorias con distribuciones independientes y de igual forma tiende a seguir una distribución normal.

En otras palabras, el TLC nos dice que si tomamos distintas muestras de una población y calculamos la media de cada una de ellas, estas medias se distribuirán alrededor de la media poblacional según una distribución normal. Además, cuanto mayor sea el tamaño de las muestras, más se acercará esta distribución a una forma de campana simétrica.

La importancia del TLC radica en que nos permite trabajar con distribuciones normales, las cuales son mucho más fáciles de manipular y analizar estadísticamente. Esto simplifica enormemente el cálculo de probabilidades y nos brinda herramientas para hacer inferencias sobre la población a partir de las muestras recolectadas.

Aplicaciones del Teorema del Límite Central

El TLC tiene numerosas aplicaciones en diferentes campos de estudio. Algunas de las áreas en las que se utiliza ampliamente son:

• Economía: En economía, el TLC permite modelar y predecir comportamientos económicos a través de muestras de datos. Por ejemplo, al estudiar los ingresos de una población, podemos utilizar este teorema para estimar la media y la variabilidad de los ingresos de la población en general.
• Medicina: En medicina, el TLC se utiliza para analizar resultados de ensayos clínicos o estudios epidemiológicos. Permite estimar la efectividad de un tratamiento o la prevalencia de una enfermedad en una población, entre otros análisis.
• Ingeniería: En ingeniería, el TLC es de gran utilidad para entender y modelar fenómenos aleatorios en distintas áreas, como por ejemplo el tiempo de vida útil de un material.
• Finanzas: En finanzas, el TLC es fundamental para el análisis de riesgo y para la valoración de instrumentos financieros. Por ejemplo, nos permite calcular la volatilidad de un activo financiero a partir de datos históricos.

Condiciones para aplicar el Teorema del Límite Central

Aunque el TLC es una herramienta poderosa, debemos tener en cuenta algunas condiciones para aplicarlo correctamente:

1. Tamaño muestral grande: El teorema establece que la distribución de las medias tiende a ser normal cuando el tamaño muestral es suficientemente grande (generalmente mayor a 30).
2. Distribuciones independientes e idénticas: Las variables aleatorias deben ser independientes entre sí y provenir de la misma distribución.
3. Tamaño de muestra pequeño: Aunque el TLC se cumple mejor con tamaños de muestra grandes, para muestras más pequeñas aún se obtienen aproximaciones aceptables de una distribución normal.

El Teorema del Límite Central nos proporciona las bases teóricas para analizar y comprender la variabilidad de los datos a través de la media y nos permite hacer inferencias confiables sobre la población en general. Es una herramienta esencial en estadísticas y su aplicación se extiende a múltiples campos de estudio.

Cuál es la fórmula básica del Teorema del Límite Central

El Teorema del Límite Central es uno de los conceptos fundamentales en estadística y juega un papel crucial en la comprensión de cómo se comportan las muestras aleatorias.

La fórmula básica del Teorema del Límite Central establece que, a medida que el tamaño de la muestra aumenta indefinidamente, la distribución de la media muestral se aproxima cada vez más a una distribución normal, independientemente de la forma de la distribución original.

Esta fórmula se puede expresar matemáticamente como:


Z = ( - µ) / (σ / √n)


Donde:

• Z representa la puntuación z, que es una medida estandarizada utilizada para calcular las probabilidades en una distribución normal estándar.
• es el valor de la variable aleatoria individual.
• µ es la media de la población.
• σ es la desviación estándar de la población.
• n es el tamaño de la muestra.

Esta fórmula nos permite evaluar qué tan inusual o común es un punto de datos específico dentro de una distribución normal, y nos brinda una herramienta fundamental para realizar inferencias estadísticas sobre la media de una población utilizando muestras.

Cómo se aplica el Teorema del Límite Central en la práctica

El Teorema del Límite Central es uno de los conceptos más importantes en estadística y tiene una amplia aplicación en la práctica. Esta fórmula revela el secreto detrás de las estadísticas, permitiendo realizar inferencias precisas sobre una población utilizando muestras aleatorias.

En la práctica, el Teorema del Límite Central se utiliza para construir intervalos de confianza y realizar pruebas de hipótesis. Estas son herramientas fundamentales en el análisis estadístico, ya que nos permiten tomar decisiones informadas basadas en la información que tenemos disponible.

Intervalos de confianza

Un intervalo de confianza es un rango de valores dentro del cual se espera que esté el parámetro de interés con cierto nivel de certeza. Para construir un intervalo de confianza, se selecciona una muestra aleatoria de la población y se calcula un estadístico descriptivo, como la media o la proporción.

A partir de esta muestra, se utiliza el Teorema del Límite Central para determinar la distribución muestral del estadístico. Esto significa que podemos hacer suposiciones sobre cómo se comportaría el estadístico si tomáramos múltiples muestras aleatorias de la misma población.

El Teorema del Límite Central establece que, a medida que el tamaño de la muestra aumenta, la distribución muestral del estadístico se aproxima a una distribución normal. Esto es independiente de la forma de la distribución de la población.

Utilizando la distribución normal, se puede calcular un intervalo de confianza alrededor del estadístico descriptivo. El nivel de confianza se elige previamente y representa la probabilidad de que el parámetro de interés esté contenido dentro del intervalo calculado.

Por ejemplo, si queremos estimar la media de una población con un nivel de confianza del 95%, utilizamos el Teorema del Límite Central para obtener el intervalo de confianza correspondiente. Este intervalo nos indicará con qué grado de certeza podemos afirmar que la media real de la población está contenida en ese rango.

Pruebas de hipótesis

Las pruebas de hipótesis son otra aplicación importante del Teorema del Límite Central. Estas pruebas permiten tomar decisiones sobre una afirmación hecha acerca de un parámetro poblacional, como la media o la proporción.

La primera etapa en una prueba de hipótesis es establecer una hipótesis nula y una hipótesis alternativa. La hipótesis nula generalmente representa una afirmación que desea refutar, mientras que la hipótesis alternativa representa una afirmación que desea respaldar.

A continuación, se selecciona una muestra aleatoria de la población y se calcula el estadístico relevante. Utilizando el Teorema del Límite Central, se puede determinar la distribución muestral del estadístico bajo la hipótesis nula. Esto nos permite evaluar qué tan probable es obtener un valor igual o más extremo al observado si la hipótesis nula fuera verdadera.

Con esta información, se calcula un valor de prueba y se compara con un valor crítico basado en el nivel de significancia elegido. Si el valor de prueba cae en la región crítica, se rechaza la hipótesis nula en favor de la hipótesis alternativa.

El Teorema del Límite Central es fundamental para realizar estas pruebas de hipótesis ya que nos permite hacer suposiciones sobre la distribución muestral del estadístico, lo cual es necesario para evaluar la probabilidad de observar resultados extremos bajo la hipótesis nula.

El Teorema del Límite Central tiene una amplia aplicación en la práctica estadística. A través de él, podemos construir intervalos de confianza y realizar pruebas de hipótesis que nos permiten realizar inferencias precisas sobre las poblaciones a partir de muestras aleatorias. Es una herramienta poderosa que revela el secreto detrás de las estadísticas y nos ayuda a tomar decisiones informadas basadas en datos.

Cómo afecta el tamaño de la muestra en la aplicación del Teorema del Límite Central

El Teorema del Límite Central es uno de los conceptos fundamentales en el campo de la estadística. Nos permite hacer inferencias acerca de una población a partir del análisis de muestras aleatorias. Sin embargo, para aplicar este teorema de manera precisa, es importante tener en cuenta el tamaño de la muestra.

Cuando se hace referencia al tamaño de la muestra, nos referimos a la cantidad de observaciones o datos que se analizan en un estudio estadístico. Es importante tener una muestra lo suficientemente grande como para obtener conclusiones confiables y representativas de la población objetivo.

El Teorema del Límite Central establece que, si tomamos muestras aleatorias suficientemente grandes de una población, la distribución de las medias de estas muestras se aproximará a una distribución normal, independientemente de la forma de la distribución de la población original.

En otras palabras, el tamaño de la muestra influye en la precisión con la que podemos estimar la media poblacional. Si nuestra muestra es pequeña, es más probable que nuestras estimaciones estén sesgadas y no reflejen con precisión la verdadera media de la población.

En contraste, si tenemos una muestra grande, las estimaciones serán mucho más precisas y se acercarán más a la media poblacional real. Esto se debe a que, a medida que aumenta el tamaño de la muestra, se reduce la variabilidad y se minimiza el impacto de las observaciones atípicas.

Además, con una muestra grande, también podemos hacer inferencias más sólidas sobre otros parámetros de interés, como la varianza o la proporción poblacional. Cuanto mayor sea el tamaño de la muestra, menor será la incertidumbre asociada a estas estimaciones.

Es importante destacar que aunque el Teorema del Límite Central garantiza que la distribución de las medias muestrales se aproxime a una distribución normal, no todos los datos individuales en la muestra deben seguir necesariamente una distribución normal. Esto es particularmente útil cuando trabajamos con datos no paramétricos.

El tamaño de la muestra juega un papel fundamental en la aplicación del Teorema del Límite Central. Una muestra suficientemente grande nos permite obtener estimaciones más precisas de los parámetros poblacionales y hacer inferencias más sólidas. Por lo tanto, al diseñar un estudio estadístico, debemos asegurarnos de tener un tamaño de muestra adecuado para obtener resultados confiables y representativos.

Cuáles son las implicaciones del Teorema del Límite Central en la interpretación de los resultados estadísticos

El Teorema del Límite Central es uno de los conceptos más importantes en estadística y desempeña un papel fundamental en la interpretación de los resultados obtenidos a partir de los análisis estadísticos. Este teorema nos permite comprender cómo se distribuyen las muestras de una población en particular, lo cual es crucial para tomar decisiones basadas en datos.

En términos simples, el Teorema del Límite Central establece que, independientemente de la forma de la distribución original, si tomamos muestras aleatorias suficientemente grandes de una población, la distribución de las medias de esas muestras se aproximará a una distribución normal. Esto implica que, incluso si la población original no sigue una distribución normal, podemos utilizar las propiedades de esta última para realizar inferencias estadísticas válidas sobre la población en general.

¿Pero qué significa esto en la práctica? Bueno, imagina que estás realizando un estudio para investigar el efecto de una nueva droga en la reducción de los niveles de colesterol en pacientes con enfermedad cardíaca. Recolectas datos de una muestra de 500 pacientes y calculas la media de los niveles de colesterol después de administrarles la droga. Sin embargo, la distribución de esos datos puede ser bastante asimétrica o no seguir una distribución conocida.

Aquí es donde entra en juego el Teorema del Límite Central. Supongamos que tus datos no siguen una distribución normal. A pesar de esto, debido al teorema, sabemos que la distribución de las medias de las muestras se aproximará a una distribución normal. Es decir, la media de las medias de todas las muestras tomadas se acercará a la media poblacional. Esto nos permite hacer inferencias sobre la población en general, incluso si los datos originales no siguen una distribución normal.

Si esto te parece complicado, ¡no te preocupes! La belleza del Teorema del Límite Central es que nos proporciona un marco sólido para comprender y analizar los resultados estadísticos, sin importar la forma de la distribución original. Además, este concepto es ampliamente utilizado en diferentes campos, desde la investigación científica hasta el análisis de datos en negocios y finanzas.

Inferencias válidas y confiables gracias al Teorema del Límite Central

Otra implicación importante del Teorema del Límite Central es que nos permite obtener inferencias válidas y confiables a partir de nuestras muestras. Imagina que deseas calcular un intervalo de confianza para la media de la población. Al tener una muestra lo suficientemente grande, puedes utilizar la aproximación normal y aplicar fórmulas estadísticas para estimar dicho intervalo.

El Teorema del Límite Central también tiene aplicaciones en pruebas de hipótesis. Podemos utilizar distribuciones normales debido a la propiedad antes mencionada de que cuando tenemos muestras grandes, la distribución de las medias se aproxima a una distribución normal. Por lo tanto, podemos calcular valores críticos y realizar pruebas de hipótesis teniendo en cuenta esta aproximación.

Ahora bien, es importante tener en cuenta que para que el Teorema del Límite Central funcione de manera adecuada, es necesario cumplir con ciertos supuestos, como que las muestras sean aleatorias y que el tamaño de la muestra sea lo suficientemente grande. Además, este teorema se basa en la estadística clásica y puede no aplicarse en todas las situaciones.

El Teorema del Límite Central es una herramienta fundamental en estadística que nos permite comprender cómo se distribuyen las muestras de una población, incluso si los datos originales no siguen una distribución normal. Esto tiene implicaciones importantes en la interpretación de los resultados estadísticos, permitiéndonos realizar inferencias válidas y confiables sobre la población en general. Es un concepto ampliamente utilizado en diferentes campos y forma parte esencial del kit de herramientas de todo estadístico o científico de datos.

Existen casos en los que el Teorema del Límite Central no se cumple o no es aplicable

Si bien el Teorema del Límite Central es una herramienta poderosa en el campo de las estadísticas, hay situaciones específicas en las que no se cumple o simplemente no es aplicable. Es importante reconocer estas excepciones para evitar cometer errores al utilizar este teorema en el análisis de datos.

Distribuciones no simétricas

Una de las condiciones necesarias para que el Teorema del Límite Central sea válido es que la distribución de la población sea simétrica. Esto significa que la curva de distribución debe ser igual a su imagen en un eje vertical. Sin embargo, existen casos en los que la distribución no es simétrica, como por ejemplo, la distribución asimétrica a la derecha o a la izquierda. En estos casos, el Teorema del Límite Central puede no ser adecuado para realizar inferencias estadísticas precisas.

Tamaño muestral pequeño

Otro factor a considerar es el tamaño de la muestra utilizada en el análisis de los datos. El Teorema del Límite Central establece que a medida que el tamaño de la muestra se acerca al infinito, la distribución de la media muestral se aproxima a una distribución normal. Sin embargo, cuando el tamaño muestral es pequeño, esta aproximación puede no ser válida. En estos casos, se requiere el uso de métodos alternativos para el análisis estadístico, como las pruebas no paramétricas.

Presencia de valores atípicos

Los valores atípicos, también conocidos como outliers, son observaciones que se encuentran muy alejadas del resto de los datos en una muestra o población. Estos valores extremos pueden tener un impacto significativo en los resultados del análisis estadístico y pueden influir en la validez del Teorema del Límite Central. Si se sospecha la presencia de valores atípicos en los datos, es importante realizar un análisis más detallado para evaluar su efecto en las conclusiones estadísticas.

Dependencia entre observaciones

El Teorema del Límite Central asume que las observaciones dentro de una muestra se obtienen de forma independiente. Sin embargo, en algunos casos, las observaciones pueden estar correlacionadas o depender unas de otras. Esto puede suceder, por ejemplo, cuando se recopilan datos longitudinales o datos de series temporales. La dependencia entre observaciones puede afectar la validez del Teorema del Límite Central y requerir el uso de técnicas específicas para el análisis de datos.

Si bien el Teorema del Límite Central es una herramienta poderosa en el análisis estadístico, existen ciertas situaciones en las que no se cumple o no es aplicable. Es fundamental considerar estos casos y utilizar métodos alternativos cuando sea necesario, para garantizar resultados precisos y confiables en el campo de las estadísticas.

Cuáles son las ventajas y limitaciones de utilizar el Teorema del Límite Central en estudios estadísticos

El Teorema del Límite Central es una poderosa herramienta en el campo de la estadística que permite obtener resultados confiables y precisos, incluso cuando se trabajan con muestras pequeñas o no desviadas. Sin embargo, como cualquier método estadístico, también tiene sus ventajas y limitaciones.

Ventajas del Teorema del Límite Central

Una de las principales ventajas del Teorema del Límite Central es su capacidad para generalizar los resultados obtenidos a partir de una muestra a toda la población objetivo. Esto significa que podemos extraer conclusiones sólidas sobre una población en base a datos recopilados de un subconjunto representativo.

Otra ventaja importante es que el Teorema del Límite Central nos permite trabajar con muestras pequeñas sin comprometer la confiabilidad de nuestros resultados. Esto es especialmente útil en situaciones donde obtener una muestra grande puede ser costoso o difícil de lograr.

Además, el Teorema del Límite Central es aplicable a diferentes tipos de distribuciones, lo que lo convierte en una herramienta versátil en muchos campos de estudio. Ya sea que estemos trabajando con una distribución normal, una distribución binomial o cualquier otra distribución, este teorema nos brinda una aproximación precisa para estimar los parámetros poblacionales.

Limitaciones del Teorema del Límite Central

A pesar de todas las ventajas mencionadas anteriormente, el Teorema del Límite Central también tiene algunas limitaciones que debemos tener en cuenta al momento de utilizarlo en estudios estadísticos.

En primer lugar, es importante destacar que el Teorema del Límite Central asume que las muestras son independientes y que las observaciones dentro de cada muestra son también independientes. Si estas condiciones no se cumplen, los resultados obtenidos pueden estar sesgados o poco confiables.

Otra limitación del Teorema del Límite Central es que puede no funcionar bien con tamaños de muestra extremadamente pequeños. Aunque este teorema nos permite obtener estimaciones confiables incluso con muestras pequeñas, existe un límite en cuanto a la precisión de los resultados cuando los tamaños de muestra son muy reducidos.

Además, el Teorema del Límite Central solo se aplica a distribuciones simétricas o aproximadamente simétricas. Esto significa que si estamos trabajando con una distribución sesgada, los resultados del teorema pueden ser inexactos.

Por último, debemos tener en cuenta que el Teorema del Límite Central supone que la población objetivo sigue una distribución normal o que la muestra es suficientemente grande para que la distribución tienda a parecerse a una normal. Si esta suposición no se cumple, los resultados obtenidos pueden no ser representativos o adecuados.

Aunque el Teorema del Límite Central es una herramienta poderosa y ampliamente utilizada en estudios estadísticos, es importante considerar sus ventajas y limitaciones antes de aplicarlo en un análisis particular. Al estar conscientes de estos aspectos, podremos utilizar adecuadamente este teorema y obtener resultados confiables y válidos en nuestras investigaciones.

Puedes explicar un ejemplo práctico de cómo el Teorema del Límite Central se utiliza para analizar datos

El Teorema del Límite Central es una poderosa herramienta en estadística que nos permite analizar datos y sacar conclusiones sobre la población a partir de una muestra. Para entender mejor cómo funciona este teorema, podemos recurrir a un ejemplo práctico.

Supongamos que queremos investigar la altura promedio de los estudiantes de una universidad determinada. Sería imposible medir la altura de todos los estudiantes, ya que podrían ser cientos o incluso miles. Por lo tanto, tomamos una muestra representativa de, digamos, 100 estudiantes.

Para simplificar, supongamos también que la altura de los estudiantes sigue una distribución normal, lo cual es común en muchos fenómenos naturales y sociales. Esto significa que la mayoría de los estudiantes tendrán alturas cercanas a la media y muy pocos estarán en los extremos.

Una vez que tenemos nuestra muestra de 100 estudiantes, medimos su altura y calculamos la media. Digamos que obtenemos una media de 170 cm.

Ahora viene la parte interesante. Según el Teorema del Límite Central, si repitiéramos este proceso de tomar muestras y calcular la media muchas veces, obtendríamos una distribución de las medias que se aproximaría a una distribución normal, sin importar cómo se distribuyan realmente las alturas en la población total.

Esto significa que a medida que aumentamos el tamaño de la muestra, las medias que obtenemos se vuelven cada vez más precisas y se acercan más a la verdadera media de la población. En nuestro ejemplo, esto significaría que si tomamos una muestra más grande, digamos 1000 estudiantes, y calculamos la media, es probable que obtengamos un valor más cercano a la altura promedio de todos los estudiantes de la universidad.

Este resultado es extremadamente útil en el campo de la estadística, ya que nos permite hacer inferencias sobre una población completa a partir de una muestra más pequeña. Además, también nos da una idea de la confiabilidad de nuestros resultados. Cuanto mayor sea el tamaño de la muestra, mayor será la confianza que podemos tener en nuestras conclusiones.

El Teorema del Límite Central nos proporciona una fórmula para analizar datos y estimar parámetros poblacionales a partir de muestras. Aunque su aplicación puede parecer abstracta, como vemos en este ejemplo práctico, sus implicaciones son muy relevantes en el mundo real y nos ayudan a comprender mejor el funcionamiento de las estadísticas.

El Teorema del Límite Central se aplica solo a distribuciones normales

El Teorema del Límite Central es una de las herramientas más poderosas en el campo de la estadística. Sin embargo, es importante tener en cuenta que este teorema se aplica únicamente a distribuciones normales. ¿Pero qué significa exactamente esto?

Una distribución normal, también conocida como distribución gaussiana, es un tipo de distribución de probabilidad continua que se caracteriza por su forma de campana simétrica. Esto significa que los valores tienden a agruparse alrededor de la media y la mayoría de los datos se encuentran cerca de ella, mientras que los valores extremos se vuelven menos probables a medida que nos alejamos. Esto se conoce como la propiedad de "cola pesada" de la distribución normal.

El Teorema del Límite Central establece que, dado un número suficientemente grande de muestras independientes de cualquier distribución, la distribución de las medias de esas muestras se aproximará a una distribución normal. En otras palabras, sin importar qué distribución original tengamos, si tomamos varias muestras y calculamos la media de cada una, estas medias se comportarán como una distribución normal.

Esto es de gran utilidad en el campo de la inferencia estadística, ya que nos permite utilizar la distribución normal para realizar estimaciones y tomar decisiones basadas en las medias de nuestras muestras. Es decir, podemos aplicar técnicas estadísticas basadas en la distribución normal, incluso si nuestros datos originales no siguen una distribución normal.

Es importante destacar que el tamaño de la muestra es un factor crucial para que el Teorema del Límite Central se aplique correctamente. Cuanto mayor sea el número de muestras que tomemos, más se acercarán las medias a una distribución normal. Esto se debe a que el efecto combinado de múltiples muestras tiende a eliminar cualquier comportamiento no normal presente en cada muestra individual.

El Teorema del Límite Central es una poderosa herramienta estadística que nos permite utilizar la distribución normal para realizar inferencias sobre nuestras muestras, incluso si las distribuciones originales no son normales. Sin embargo, es importante recordar que este teorema solo se aplica a distribuciones normales y que el tamaño de la muestra desempeña un papel fundamental en su aplicación exitosa.

Preguntas frecuentes (FAQ)

1. ¿Qué es el Teorema del Límite Central?

El Teorema del Límite Central es una propiedad matemática que establece que, en ciertas condiciones, la distribución de la media de un conjunto grande de muestras se aproxima a una distribución normal.

2. ¿Por qué es importante el Teorema del Límite Central?

El Teorema del Límite Central es importante porque permite hacer inferencias estadísticas sobre una población basándose en una muestra. Además, muchas técnicas y pruebas estadísticas se basan en este teorema.

3. ¿Cuáles son las condiciones necesarias para aplicar el Teorema del Límite Central?

Las condiciones necesarias para aplicar el Teorema del Límite Central son que las observaciones sean independientes y que la muestra sea lo suficientemente grande (generalmente se acepta un tamaño de muestra mayor o igual a 30).

4. ¿En qué situaciones se utiliza el Teorema del Límite Central?

El Teorema del Límite Central se utiliza en diversas áreas como la economía, la medicina, la psicología y cualquier campo donde se realicen estudios con muestras y se desee hacer inferencias estadísticas sobre la población.

5. ¿Cómo afecta el tamaño de muestra al Teorema del Límite Central?

A mayor tamaño de muestra, la distribución de la media se aproximará más a una distribución normal. Esto implica que los resultados serán más precisos y confiables en muestras grandes.