Dominio de una función cuadrática: Todo lo que debes saber para obtener resultados precisos

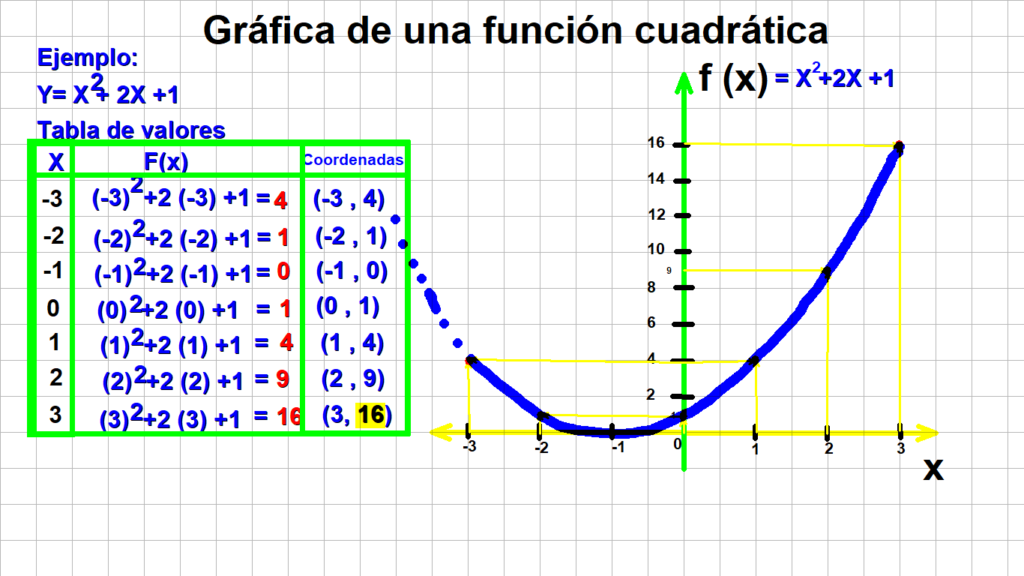
El dominio de una función es uno de los conceptos fundamentales en el estudio del álgebra y el cálculo. Se refiere al conjunto de valores para los cuales la función está definida y puede generar un resultado específico. En el caso particular de las funciones cuadráticas, que son de la forma f(x) = ax^2 + bx + c, conocer su dominio es fundamental para comprender su comportamiento y realizar cálculos precisos.

Exploraremos en detalle qué significa el dominio de una función cuadrática y cómo determinarlo correctamente. Veremos cómo los coeficientes a, b y c afectan directamente estos valores permitidos y analizaremos algunos ejemplos prácticos para facilitar su comprensión. También abordaremos situaciones especiales como funciones con raíces complejas o funciones con restricciones adicionales. Al finalizar la lectura, tendrás las herramientas necesarias para identificar rápidamente el dominio de cualquier función cuadrática y resolver problemas relacionados con confianza y precisión.

Qué es una función cuadrática y cómo se representa matemáticamente

Una función cuadrática es un tipo de función matemática que se expresa mediante una ecuación de segundo grado. Estas funciones son muy utilizadas en álgebra y cálculo, ya que permiten modelar una amplia variedad de fenómenos naturales y sociales.

La forma general de una función cuadrática es: f(x) = ax^2 + bx + c, donde a, b y c son constantes numéricas y x representa la variable independiente.

En esta ecuación, el término ax^2 representa el coeficiente principal, que determina la concavidad de la parábola. Si a es positivo, la parábola se abrirá hacia arriba, mientras que si a es negativo, la parábola se abrirá hacia abajo.

Por su parte, el término bx es el coeficiente lineal y el término c representa el término independiente. Estos dos términos influyen en la posición de la parábola en el plano cartesiano.

Cómo graficar una función cuadrática

Para graficar una función cuadrática, es necesario seguir algunos pasos:

1. Paso 1: Identificar los valores de a, b y c en la ecuación dada.
2. Paso 2: Calcular el vértice de la parábola utilizando la fórmula x = -b/2a y sustituyendo este valor en la ecuación original para obtener el valor correspondiente de y.
3. Paso 3: Determinar los puntos adicionales necesarios para trazar la parábola. Estos puntos se pueden obtener al evaluar la función cuadrática para diferentes valores de x.
4. Paso 4: Graficar los puntos obtenidos y trazar la parábola que los conecta. Se recomienda utilizar una regla y un compás para obtener curvas suaves y precisas.

Es importante recordar que la representación gráfica de una función cuadrática es siempre una parábola, ya sea abierta hacia arriba o hacia abajo. La concavidad y la posición de la parábola dependen de los coeficientes a, b y c.

Cuál es la forma general de una función cuadrática y cómo se puede simplificar

Una función cuadrática es una ecuación algebraica que puede ser escrita en la forma general f(x) = ax^2 + bx + c, donde a, b y c son coeficientes numéricos.

La forma general permite representar gráficamente una función cuadrática mediante una parábola, la cual puede abrir hacia arriba (si a es positivo) o hacia abajo (si a es negativo).

A veces, la forma general de una función cuadrática puede resultar complicada de manejar y dificultar algunos cálculos o interpretaciones. Por esto, es común simplificar la forma general utilizando otras dos formas equivalentes: la forma vértice y la forma factorizada.

La forma vértice de una función cuadrática

La forma vértice de una función cuadrática se obtiene completando el cuadrado de la expresión polinómica. Esta forma se expresa como f(x) = a(x - h)^2 + k, donde (h, k) representa las coordenadas del vértice de la parábola.

Al utilizar la forma vértice, la función cuadrática se simplifica y se obtiene una mayor comprensión del comportamiento de la parábola. Además, con esta forma es más sencillo identificar el eje de simetría y los valores máximo o mínimo de la función.

La forma factorizada de una función cuadrática

La forma factorizada de una función cuadrática se obtiene factorizando la expresión polinómica en los términos (x - r), donde r son las raíces de la función. Esta forma se expresa como f(x) = a(x - r1)(x - r2).

La forma factorizada permite identificar rápidamente las raíces de la función, es decir, los valores de x para los cuales la función se anula. Al conocer estas raíces, se puede determinar el comportamiento de la parábola y si corta o no al eje x.

Es importante recordar que las tres formas (general, vértice y factorizada) son equivalentes entre sí y contienen la misma información sobre la función cuadrática. La elección de la forma a utilizar dependerá del contexto y de la información específica que se requiera en cada caso.

Qué es el dominio de una función y cómo se determina en una función cuadrática

El dominio de una función es el conjunto de todos los valores para los cuales la función está definida. En el caso de las funciones cuadráticas, estas se representan en la forma f(x) = ax^2 + bx + c, donde a, b y c son constantes y x es la variable independiente.

Para determinar el dominio de una función cuadrática, debemos tener en cuenta que no todas las valores de x serán válidos ya que podrían resultar en divisiones entre cero o raíces cuadradas de números negativos, lo cual no estaría definido en el conjunto de números reales.

Reglas para determinar el dominio de una función cuadrática

Existen algunas reglas generales que podemos seguir para determinar el dominio de una función cuadrática:

• El dominio de una función cuadrática siempre será todo el conjunto de números reales, a menos que se presente alguna restricción explícita.
• Si la función cuadrática está escrita en la forma general f(x) = ax^2 + bx + c, el dominio será todo el conjunto de números reales, ya que no existen operaciones que restrinjan los valores posibles de x.
• Si la función cuadrática contiene algún tipo de restricción explícita, como una división por cero o una raíz cuadrada de un número negativo, entonces el dominio estará restringido a los valores de x que no violen dicha restricción.
• En el caso de una división por cero, debemos buscar los valores de x que hagan que el denominador sea igual a cero y excluirlos del dominio. Esto se debe a que no podemos dividir entre cero.
• Si la función cuadrática contiene una raíz cuadrada, debemos buscar los valores de x que hagan que el radicando sea mayor o igual a cero, ya que no podemos calcular la raíz cuadrada de un número negativo en el conjunto de números reales.

Asegurarse de determinar correctamente el dominio de una función cuadrática es crucial para obtener resultados precisos y evitar errores matemáticos. Al seguir las reglas mencionadas y prestar atención a posibles restricciones explícitas, podrás determinar con precisión el conjunto de valores de x para los cuales la función está definida y poder realizar cálculos y análisis adecuados.

Cuál es la importancia del dominio en una función cuadrática y qué información nos proporciona

El dominio en una función cuadrática es de vital importancia, ya que nos permite determinar qué valores de entrada son válidos y nos brinda información fundamental sobre la relación entre las variables involucradas.

En el contexto de las funciones cuadráticas, el dominio se refiere al conjunto de valores posibles para la variable independiente (x). Estos valores deben ser aquellos que no generen divisiones por cero ni violen las restricciones impuestas por la función.

Para comprender mejor el concepto, recordemos que una función cuadrática tiene la forma general f(x) = ax^2 + bx + c, donde a, b y c son constantes conocidas. El objetivo es encontrar los valores de x para los cuales esta función esté definida, es decir, aquellos valores que no generen ninguna inconsistencia o contradicción matemática.

En primer lugar, es importante mencionar que una función cuadrática está definida para todos los números reales, es decir, su dominio es el conjunto de todos los números reales (-∞, +∞). Sin embargo, existen casos especiales en los que la función puede tener restricciones adicionales en su dominio.

Posibles restricciones en el dominio

Una de las restricciones más comunes en el dominio de una función cuadrática ocurre cuando tenemos una raíz cuadrada en la expresión. Sabemos que la raíz cuadrada de un número negativo no está definida en el conjunto de los números reales, por lo tanto, debemos evitar aquellos valores de x que hagan que la expresión dentro de la raíz sea negativa. De esta forma, podemos establecer una restricción en el dominio de la función.

ax^2 + bx + c ≥ 0

Esta desigualdad nos permite determinar qué valores de x satisfacen la condición de no tener una raíz cuadrada negativa. Para encontrar los intervalos donde la función es no negativa, podemos utilizar diferentes métodos como el análisis del discriminante o graficar la función y observar los puntos en los que intersecta el eje x.

Otra posible restricción ocurre cuando tenemos una fracción en la función cuadrática. Sabemos que las divisiones por cero están indefinidas, por lo tanto, debemos evitar aquellos valores de x que hagan que el denominador de la fracción sea igual a cero. Esta restricción nos permite determinar qué valores de x provocan una división por cero y, por lo tanto, están excluidos del dominio de la función.

b ≠ 0

En este caso, debemos asegurarnos de que el valor de b sea diferente de cero para evitar divisiones por cero. Podemos discernir esta restricción analizando la ecuación de la función y encontrando los valores de x que anulan el denominador.

Además de estas restricciones comunes, es importante considerar cualquier otra limitación específica impuesta por el contexto del problema o la naturaleza de la función cuadrática en cuestión. El dominio de una función cuadrática puede variar según cada situación particular, por lo que es fundamental analizar detenidamente todas las posibles restricciones y condiciones que se puedan presentar.

El dominio en una función cuadrática nos permite establecer los valores válidos de entrada y nos brinda información valiosa sobre la relación entre las variables involucradas. Es fundamental considerar diferentes restricciones que pueden surgir a partir de raíces cuadradas o divisiones por cero para determinar el dominio adecuado de la función.

Un análisis exhaustivo del dominio nos ayudará a obtener resultados precisos y evitar errores matemáticos al trabajar con funciones cuadráticas. Recordemos siempre ser cuidadosos al identificar las restricciones y condiciones particulares de cada función, ya que estas pueden variar dependiendo del contexto del problema.

Cuáles son las restricciones del dominio en una función cuadrática y cómo se pueden identificar

Una función cuadrática es una ecuación de la forma f(x) = ax^2 + bx + c, donde a, b y c son constantes y a no puede ser igual a cero. El dominio de una función representa el conjunto de todos los valores de x para los cuales la función tiene un valor definido.

En una función cuadrática, no hay restricciones específicas en el dominio, ya que la función está definida para cualquier valor de x en los números reales. Sin embargo, es importante tener en cuenta que algunos valores de x podrían hacer que la función sea igual a cero o causar divisiones por cero en el caso de denominadores.

Para identificar las restricciones del dominio en una función cuadrática, es necesario considerar dos casos: cuando el coeficiente 'a' es diferente de cero y cuando es igual a cero.

Cuando 'a' es diferente de cero

En este caso, la función cuadrática tiene un eje de simetría vertical dado por la línea x = -b/2a. Esto significa que el vértice de la parábola, que es el punto mínimo o máximo de la función, se encuentra en esa línea vertical.

El dominio de la función cuadrática es (-∞, +∞), lo que indica que la función está definida para todos los valores reales de x.

Cuando 'a' es igual a cero

Si el coeficiente 'a' es igual a cero, la función cuadrática se reduce a una función lineal de la forma f(x) = bx + c. En este caso, la función es una línea recta y su dominio también es (-∞, +∞), lo que significa que está definida para todos los valores reales de x.

El dominio de una función cuadrática siempre será (-∞, +∞), independientemente del coeficiente 'a'. Es importante recordar que las restricciones del dominio podrían existir en otros tipos de funciones, pero no en una función cuadrática.

Qué estrategias se pueden utilizar para encontrar el dominio de una función cuadrática

El dominio de una función cuadrática es el conjunto de todos los valores de entrada para los cuales la función está definida. En otras palabras, son los valores de x para los cuales la función tiene sentido y podemos calcular su valor correspondiente.

Existen diversas estrategias que podemos utilizar para encontrar el dominio de una función cuadrática. A continuación, describiré algunas de las más comunes:

1. Analizar el coeficiente principal

El coeficiente principal de una función cuadrática es el coeficiente que acompaña al término cuadrático (x^2). Si este coeficiente es distinto de cero, entonces la función tendrá dominio en todos los números reales, ya que no habrá restricciones en cuanto a los valores de x. En este caso, el dominio sería (-∞, +∞).

2. Resolver desigualdades

Otra estrategia para encontrar el dominio de una función cuadrática es resolver desigualdades. Para ello, se puede plantear una desigualdad teniendo en cuenta que la función cuadrática puede tener un vértice que represente un mínimo o un máximo. Dependiendo de esa situación, se puede determinar si hay restricciones en cuanto a los valores de x. Por ejemplo, si la función tiene un vértice mínimo y abre hacia arriba, el dominio sería (-∞, +∞).

3. Observar los puntos críticos

Los puntos críticos de una función son aquellos en los cuales la derivada de la función es cero o no está definida. Estos puntos pueden ayudarnos a determinar las restricciones en cuanto al dominio de la función. Por ejemplo, si la función tiene un punto crítico en x = a, entonces el dominio de la función estaría restringido a todos los números reales excepto a.

4. Verificar la existencia de raíces imaginarias

En algunos casos, una función cuadrática puede tener raíces imaginarias, es decir, soluciones que no pertenecen al conjunto de los números reales. Si esto ocurre, el dominio de la función estaría restringido a un subconjunto de los números reales.

5. Considerar situaciones particulares

En ocasiones, podemos encontrarnos con situaciones particulares que requieren un análisis más detallado para determinar el dominio de una función cuadrática. Por ejemplo, si la función incluye radicales o fracciones, podríamos tener restricciones adicionales en cuanto a los valores de x.

Encontrar el dominio de una función cuadrática puede requerir el uso de diferentes estrategias, como analizar el coeficiente principal, resolver desigualdades, observar los puntos críticos, verificar la existencia de raíces imaginarias y considerar situaciones particulares. Al aplicar estas estrategias, podemos obtener resultados precisos y determinar los valores de x para los cuales la función tiene sentido.

Cómo se puede representar gráficamente el dominio de una función cuadrática

Para representar gráficamente el dominio de una función cuadrática, es necesario comprender primero qué es el dominio de una función y cómo se relaciona con las funciones cuadráticas.

El dominio de una función se refiere al conjunto de todos los valores posibles de entrada, o valores de x, para los cuales la función está definida. En otras palabras, es el conjunto de valores para los cuales la función tiene sentido y produce un resultado válido.

Cuando se trata de funciones cuadráticas, su dominio suele ser todo el conjunto de números reales

, a menos que haya restricciones explícitas.

La forma general de una función cuadrática es f(x) = ax^2 + bx + c, donde a, b y c son constantes. Esta función representa una parábola en un plano cartesiano.

Para determinar el dominio de una función cuadrática, es necesario tener en cuenta algunas consideraciones:

• Las funciones cuadráticas son válidas para cualquier valor real de x, ya que no hay divisiones por cero ni raíces cuadradas de números negativos involucrados.
• Si existen restricciones adicionales en el contexto del problema o la aplicación específica, es posible que se limite el dominio de la función cuadrática. Estas restricciones pueden establecerse en términos de situaciones físicas, como tiempos negativos o alturas mínimas.

Cuando se grafica una función cuadrática, su dominio se extiende desde menos infinito hasta más infinito, lo que significa que la parábola puede tener intersecciones con el eje x en cualquier punto.

El dominio de una función cuadrática es generalmente todo el conjunto de números reales, a menos que existan restricciones específicas. Al representar gráficamente una función cuadrática, podemos ver cómo se extiende a lo largo del eje x y determinar los puntos donde intersecta dicho eje.

Qué ocurre cuando el valor del parámetro `a` en una función cuadrática se acerca a cero o tiende al infinito

Al estudiar la función cuadrática en matemáticas, es importante comprender cómo se comporta cuando el valor del parámetro `a` se acerca a cero o tiende al infinito. Estos casos especiales nos brindan información valiosa sobre la forma y características de la gráfica de la función.

Cuando `a` se acerca a cero

Cuando el valor del parámetro `a` en una función cuadrática se acerca a cero, la gráfica de la función se "aplana" cada vez más cerca del eje x. Esto significa que la curva se vuelve menos pronunciada y se acerca a una línea recta horizontal.

De manera más precisa, si tenemos una función cuadrática de la forma f(x) = ax^2 + bx + c y hacemos que el valor de a se acerque a cero, entonces la ecuación se reduce a f(x) = bx + c, lo cual representa una función lineal.

En términos de la gráfica, este fenómeno implica que a medida que `a` tiende a cero, la curva se vuelve gradualmente más plana, hasta que finalmente se convierte en una línea recta.

Cuando `a` tiende al infinito

Por otro lado, cuando el valor del parámetro `a` en una función cuadrática tiende al infinito (positivo o negativo), la gráfica se abre cada vez más.

En este caso, la curva se aleja del eje x en ambas direcciones mientras `a` aumenta indefinidamente. Cuanto mayor sea el valor de `a`, más rápida y pronunciadamente se abrirá la parábola.

Si consideramos una función cuadrática f(x) = ax^2 + bx + c donde a tiende al infinito, se puede apreciar que la gráfica tendrá un comportamiento similar a una "U" invertida extendida verticalmente hacia arriba o hacia abajo, según el signo de `a`.

Estos casos límite en el dominio de las funciones cuadráticas nos permiten entender cómo la variación del parámetro `a` influye en la forma y dirección de la gráfica. Son herramientas poderosas para analizar y comprender cualquier función cuadrática, así como para estimar su comportamiento general sin necesidad de realizar cálculos adicionales.

Cuando el valor de `a` en una función cuadrática se acerca a cero, la gráfica se vuelve más plana y se aproxima a una línea recta horizontal. Por otro lado, cuando `a` tiende al infinito, la gráfica se abre cada vez más, creando una forma similar a una "U" invertida. Estos casos extremos nos brindan información valiosa sobre las características y tendencias generales de cualquier función cuadrática.

Cuál es la relación entre el dominio y los puntos críticos de una función cuadrática

El dominio de una función cuadrática está estrechamente relacionado con los puntos críticos de la misma. Para comprender esta relación, es importante primero entender qué es el dominio y los puntos críticos en el contexto de las funciones cuadráticas.

Dominio de una función cuadrática

El dominio de una función es el conjunto de todos los valores de entrada para los cuales la función está definida. En otras palabras, son los valores de "x" para los cuales podemos evaluar la función sin obtener un resultado indeterminado o no válido.

En el caso específico de las funciones cuadráticas, que se representan en la forma general f(x) = ax² + bx + c, el dominio siempre será el conjunto de números reales, ya que no hay restricciones explícitas sobre los valores de "x". Esto se debe a que las funciones cuadráticas son polinomios de grado 2 y están definidas para cualquier número real. Por lo tanto, su dominio es ilimitado.

Puntos críticos de una función cuadrática

Los puntos críticos de una función cuadrática son aquellos en los que la pendiente de la curva cambia significativamente. Estos puntos pueden ser máximos o mínimos relativos y se encuentran en las coordenadas (x, f(x)).

Para encontrar los puntos críticos de una función cuadrática, es necesario derivar la función con respecto a "x" y encontrar los valores de "x" para los cuales la derivada se iguala a cero. Estos valores de "x" corresponden a los puntos donde la pendiente de la función es igual a cero, lo que indica un cambio en la dirección de la curva.

• Si la derivada segunda de la función (f''(x)) es positiva en el punto crítico, este será un mínimo relativo.
• Si la derivada segunda de la función (f''(x)) es negativa en el punto crítico, este será un máximo relativo.

Es importante tener en cuenta que los puntos críticos solo pueden existir dentro del dominio de la función. Si hay alguna restricción sobre los valores de "x", como una raíz cuadrada con argumento negativo, entonces eso limitará el dominio y, por lo tanto, los posibles puntos críticos.

Relación entre el dominio y los puntos críticos

La relación entre el dominio y los puntos críticos de una función cuadrática radica en el hecho de que los puntos críticos solo pueden existir dentro del dominio de la función. Si hay alguna restricción en el dominio de la función, como valores que hagan que el discriminante de la función sea negativo, entonces esto afectará la existencia de los puntos críticos.

Por ejemplo, si el dominio de la función cuadrática está restringido a los números reales mayores o iguales a cero (x ≥ 0) debido a la presencia de una raíz cuadrada en la función, entonces cualquier punto crítico que se encuentre fuera de ese rango no tendrá sentido en el contexto de la función. Por lo tanto, es importante considerar tanto el dominio como los puntos críticos al realizar análisis y cálculos relacionados con una función cuadrática.

El dominio de una función cuadrática es el conjunto de todos los valores de "x" para los cuales la función está definida, y los puntos críticos son aquellos en los que la pendiente de la curva cambia significativamente. Los puntos críticos solo pueden existir dentro del dominio de la función, por lo que es importante considerar tanto el dominio como los puntos críticos al analizar y resolver problemas relacionados con funciones cuadráticas.

Qué herramientas o recursos tecnológicos se pueden utilizar para investigar y conocer más sobre el dominio de una función cuadrática

El dominio de una función cuadrática es uno de los conceptos clave en el estudio del álgebra y las matemáticas. Comprender cómo determinar el dominio de una función cuadrática es fundamental para obtener resultados precisos en problemas y ecuaciones relacionadas con esta importante rama de las matemáticas.

1. Utilizar calculadoras gráficas

Una de las herramientas más útiles y accesibles para investigar y conocer más sobre el dominio de una función cuadrática son las calculadoras gráficas. Estas calculadoras permiten representar gráficamente las funciones cuadráticas y observar cómo varía su dominio al cambiar los parámetros de la función.

Existen diversas calculadoras gráficas disponibles tanto en forma de hardware como en forma de aplicaciones móviles y programas de software. Al utilizar estas calculadoras, puedes ingresar la función cuadrática y visualizar su gráfica de manera rápida y sencilla.

Al observar la gráfica, podrás identificar los valores de x para los cuales la función está definida y, por lo tanto, determinar el dominio de la función cuadrática.

2. Aplicaciones de software especializadas

Otra opción para investigar y conocer más sobre el dominio de una función cuadrática es utilizar aplicaciones de software especializadas en el estudio de las matemáticas y el álgebra.

Estas aplicaciones suelen ofrecer una amplia gama de herramientas y recursos que te permiten explorar, analizar y resolver problemas relacionados con las funciones cuadráticas. Algunas de estas aplicaciones incluso incluyen tutoriales interactivos que te guían paso a paso en el proceso de determinar el dominio de una función cuadrática.

Además, estas aplicaciones pueden ser especialmente útiles para aquellos estudiantes que deseen practicar y afianzar sus conocimientos sobre el tema. Al permitir la resolución de ejercicios y problemas específicos relacionados con el dominio de las funciones cuadráticas, estas aplicaciones brindan una excelente oportunidad para poner en práctica los conceptos aprendidos.

3. Recursos en línea y tutoriales

La era digital nos ha proporcionado un acceso casi ilimitado a recursos en línea y tutoriales que pueden ayudarnos a investigar y conocer más sobre el dominio de una función cuadrática.

Existen numerosos sitios web, plataformas educativas y canales de video en línea que ofrecen contenido didáctico sobre las funciones cuadráticas y su dominio. Estos recursos suelen incluir explicaciones detalladas, ejemplos resueltos y ejercicios prácticos, lo que te permite aprender y practicar a tu propio ritmo.

Además, también puedes encontrar tutoriales en línea donde expertos en matemáticas y álgebra explican los conceptos clave relacionados con el dominio de las funciones cuadráticas. Estos tutoriales pueden ser de gran utilidad para aquellos que prefieren la enseñanza visual y auditiva.

4. Libros de texto y material impreso

Aunque vivimos en la era digital, los libros de texto y el material impreso siguen siendo una valiosa fuente de información y conocimiento. Existen numerosos libros de texto y recursos impresos que cubren el tema del dominio de las funciones cuadráticas de manera exhaustiva.

Estos libros suelen ofrecer explicaciones claras y concisas sobre los conceptos y técnicas necesarios para determinar el dominio de una función cuadrática. Además, muchos de ellos incluyen ejercicios y problemas prácticos con soluciones detalladas, lo que te permite practicar y reforzar tus habilidades en este ámbito.

5. Consultar a profesores y expertos en matemáticas

Finalmente, si tienes preguntas específicas o deseas profundizar aún más en el tema del dominio de las funciones cuadráticas, siempre puedes recurrir a profesores y expertos en matemáticas.

Los profesores cuentan con conocimientos sólidos y experiencia en la enseñanza de las matemáticas y pueden proporcionarte información adicional y resolver tus dudas de manera personalizada. Además, también pueden sugerirte recursos adicionales e incluso recomendarte actividades prácticas para mejorar tus habilidades en la determinación del dominio de las funciones cuadráticas.

Existen diversas herramientas y recursos tecnológicos que puedes utilizar para investigar y conocer más sobre el dominio de una función cuadrática. Ya sea utilizando calculadoras gráficas, aplicaciones de software especializadas, recursos en línea y tutoriales, libros de texto o consultando a profesores y expertos en matemáticas, tienes a tu disposición una amplia gama de opciones para obtener resultados precisos en el estudio y análisis de las funciones cuadráticas.

Existen situaciones en la vida diaria en las que el conocimiento del dominio de una función cuadrática sea útil

El dominio de una función cuadrática es un concepto fundamental en el estudio de las matemáticas, y su comprensión puede resultar especialmente útil en situaciones de la vida diaria. Una función cuadrática se define como aquella cuya ecuación tiene la forma f(x) = ax^2 + bx + c, donde a, b y c son coeficientes reales y a≠0.

El dominio de una función cuadrática es el conjunto de todos los valores de x para los cuales la función está definida. En otras palabras, es el conjunto de valores que pueden ser sustituidos en la ecuación sin generar una indeterminación o una solución imaginaria.

¿Por qué es importante conocer el dominio de una función cuadrática?

Saber determinar el dominio de una función cuadrática es crucial para diversos aspectos de la vida cotidiana, como por ejemplo, en el campo de la economía, la física, la ingeniería y la estadística. En cada una de estas áreas, los conceptos matemáticos juegan un papel fundamental en la resolución de problemas y la toma de decisiones.

En economía, por ejemplo, el dominio de una función cuadrática puede ayudar a modelar y predecir fenómenos relacionados con la oferta y demanda de productos, así como la maximización de beneficios o la minimización de costos. Conocer los límites del dominio puede evitar caer en situaciones no viables o inalcanzables en el mercado.

En el ámbito de la física, el dominio de una función cuadrática permite describir y entender el movimiento de objetos en trayectorias parabólicas, como la trayectoria de un proyectil o la forma de un fluido en caída libre. Estas situaciones son comunes tanto en la vida cotidiana como en campos especializados, y conocer el dominio de la función ayuda a comprender mejor su comportamiento físico.

En la ingeniería, el dominio de una función cuadrática es esencial en el diseño y análisis de estructuras, circuitos eléctricos o sistemas mecánicos. En estos casos, es necesario garantizar que los valores utilizados en las ecuaciones sean válidos y no generen soluciones erróneas o indeterminadas. Conocer el dominio de una función cuadrática permite establecer restricciones claras y precisas para evitar errores en estos campos de aplicación.

Además, en estadística, el dominio de una función cuadrática se utiliza en el análisis de datos y la construcción de modelos predictivos. Al determinar la relación entre variables y ajustar una función cuadrática, es necesario establecer el rango de valores permitidos para una variable. De esta manera, se pueden realizar estimaciones más precisas y confiables sobre fenómenos observados.

El dominio de una función cuadrática es un concepto fundamental que tiene aplicaciones prácticas en distintos campos de estudio y actividades cotidianas. Su comprensión y correcta interpretación nos permite tomar decisiones informadas y resolver problemas con mayor precisión. Por lo tanto, es importante adquirir el conocimiento necesario para identificar y calcular el dominio de una función cuadrática en diferentes contextos.

Cómo se puede aplicar el dominio de una función cuadrática en problemas de optimización o modelado matemático

El dominio de una función cuadrática es un concepto fundamental en el ámbito de las matemáticas. Su comprensión y aplicación son esenciales para resolver problemas de optimización y modelado matemático.

En términos generales, el dominio de una función cuadrática corresponde al conjunto de todos los valores de entrada o valores de 'x' para los cuales la función está definida. Para determinar el dominio de una función cuadrática, se deben considerar algunas restricciones que surgen de la propia naturaleza de estas funciones.

Una función cuadrática se define mediante una ecuación de la forma y = ax^2 + bx + c, donde 'a', 'b' y 'c' son constantes. La principal característica de las funciones cuadráticas es que su gráfica tiene forma de parábola.

Restricciones en el dominio

Existen dos principales restricciones a tener en cuenta al calcular el dominio de una función cuadrática:

1. Requisito de existencia: Para que una función cuadrática esté definida, el valor bajo el radical de la fórmula general debe ser mayor o igual a cero. Esto garantiza que no haya raíces imaginarias en la solución.
2. División por cero: Las funciones cuadráticas pueden presentar una restricción adicional en su dominio debido a la presencia de denominadores en fracciones. Si alguna de estas fracciones tiene un denominador igual a cero, entonces esa función no estará definida en ese punto, y ese valor de 'x' debe excluirse del dominio.

Para aplicar el dominio de una función cuadrática en problemas de optimización o modelado matemático, es crucial analizar estas restricciones y determinar el conjunto de valores para los cuales la función es válida. Esto permitirá obtener resultados precisos y evitar errores en los cálculos.

En problemas de optimización, el dominio de una función cuadrática puede ayudar a identificar los puntos de máximo o mínimo de dicha función. Estos puntos extremos son de gran interés en diversos campos, como la física, la economía o la ingeniería, ya que representan situaciones óptimas o críticas.

Por otro lado, en el modelado matemático, el dominio de una función cuadrática permite establecer límites y rangos de validez para las variables involucradas en el modelo. Esto es fundamental para interpretar y extrapolar los resultados obtenidos mediante la función cuadrática.

Ejemplo práctico

Supongamos que queremos modelar la trayectoria de un objeto lanzado al aire. Para ello, podemos utilizar una función cuadrática que describa la altura del objeto en función del tiempo.

f(t) = -gt^2 + vt + h

Donde 'g' representa la aceleración debido a la gravedad, 'v' es la velocidad inicial del objeto y 'h' es la altura inicial desde la cual se lanza.

En este caso, el dominio de la función estará dado por los valores de 't' para los cuales la función tiene sentido físico. Por ejemplo, no tendría sentido calcular la altura del objeto para valores de tiempo negativos o mayores a un determinado límite. Estos límites estarán determinados por el contexto del problema y las restricciones físicas.

Es importante tener en cuenta que el dominio de una función cuadrática puede variar dependiendo del contexto y las restricciones específicas de cada problema. Por lo tanto, es fundamental analizar cuidadosamente cada situación y considerar las limitaciones y requisitos particulares antes de aplicar el dominio en problemas de optimización o modelado matemático.

Preguntas frecuentes (FAQ)

1. ¿Cómo puedo encontrar el dominio de una función cuadrática?

Para encontrar el dominio de una función cuadrática, debes asegurarte de que no haya valores de x que hagan que el denominador de la función sea igual a cero.

2. ¿El dominio de una función cuadrática siempre es todo el conjunto de los números reales?

No, el dominio de una función cuadrática puede ser limitado si hay algún valor de x que haga que el denominador sea igual a cero o si hay alguna restricción explícita en la función.

3. ¿Qué sucede si hay un valor absoluto dentro de la función cuadrática?

Si hay un valor absoluto dentro de la función cuadrática, debes asegurarte de que el contenido del valor absoluto sea mayor o igual a cero para cualquier valor de x en el dominio de la función.

4. ¿Qué ocurre cuando hay una raíz cuadrada dentro de la función cuadrática?

Si hay una raíz cuadrada dentro de la función cuadrática, debes asegurarte de que el radicando sea mayor o igual a cero para cualquier valor de x en el dominio de la función.

5. ¿Puedo usar el método gráfico para encontrar el dominio de una función cuadrática?

Sí, puedes utilizar el método gráfico para identificar cualquier posible valor de x para el cual la función no esté definida. Sin embargo, también es importante verificar otras restricciones explícitas que pueda haber en la función.