Descubre qué cuadrilátero no tiene ejes de simetría y desafía tus conocimientos en geometría

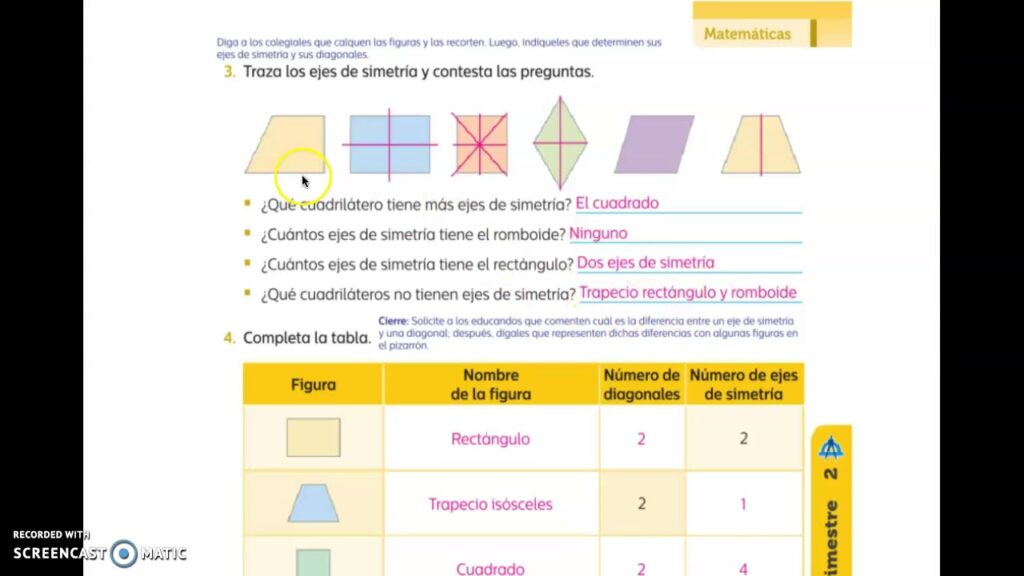
En el estudio de la geometría, los cuadriláteros son figuras planas que están formadas por cuatro lados y cuatro vértices. Entre los diferentes tipos de cuadriláteros, existen algunos que poseen ejes de simetría, es decir, líneas que dividen a la figura en dos partes iguales al reflejarla. Sin embargo, hay un tipo de cuadrilátero que no cuenta con ningún eje de simetría.

Exploraremos qué cuadrilátero no tiene ejes de simetría y analizaremos las propiedades y características que lo diferencian de otros cuadriláteros. También veremos algunos ejemplos prácticos de esta figura y su aplicación en el mundo real. ¡Prepárate para desafiar tus conocimientos en geometría y descubrir más sobre este intrigante cuadrilátero!

Cuáles son los cuadriláteros que no tienen ejes de simetría

En geometría, existen diferentes tipos de cuadriláteros que pueden clasificarse según sus características, como sus lados y ángulos. Uno de los aspectos interesantes de estos polígonos es la presencia o ausencia de ejes de simetría.

¿Qué es un eje de simetría?

Un eje de simetría es una línea imaginaria que divide una figura en dos partes idénticas cuando se refleja a lo largo de dicho eje. En otras palabras, si una figura tiene un eje de simetría, las dos mitades de la figura son perfectamente iguales y se pueden superponer exactamente.

Existen varios tipos de ejes de simetría: horizontal, vertical y oblicuo. En el caso de los cuadriláteros, nos enfocaremos en los ejes de simetría vertical y horizontal.

Cuadriláteros con ejes de simetría

Algunos cuadriláteros tienen ejes de simetría y pueden dividirse en dos partes iguales al ser reflejados a lo largo de ese eje. Estos cuadriláteros incluyen el rectángulo, el cuadrado y el rombo. Cada uno de ellos tiene al menos un eje de simetría.

• Rectángulo: este cuadrilátero tiene dos ejes de simetría, uno vertical y otro horizontal. Al ser reflejado a lo largo de estos ejes, las dos mitades del rectángulo se superponen de manera exacta.
• Cuadrado: el cuadrado es un tipo especial de rectángulo que también tiene dos ejes de simetría, uno vertical y otro horizontal. Al igual que el rectángulo, las dos mitades del cuadrado se superponen perfectamente cuando se refleja a lo largo de estos ejes.
• Rombo: el rombo es otro cuadrilátero que cuenta con ejes de simetría. En este caso, el rombo tiene un eje de simetría vertical y otro horizontal. Al ser reflejado a lo largo de estos ejes, las dos mitades del rombo se superponen de manera exacta.

Cuadriláteros sin ejes de simetría

Por otro lado, existen cuadriláteros que no tienen ejes de simetría. Esto significa que no se pueden dividir en dos partes idénticas al ser reflejados a lo largo de una línea imaginaria. Estos cuadriláteros incluyen el trapezoide y el trapecio escaleno.

• Trapezoide: el trapezoide es un cuadrilátero con solo un par de lados paralelos. La ausencia de ejes de simetría se debe a la asimetría de sus lados y ángulos. Al no tener ejes de simetría, el trapezoide no se puede dividir en dos partes iguales al ser reflejado.
• Trapecio escaleno: similar al trapezoide, el trapecio escaleno también carece de ejes de simetría debido a la asimetría de sus lados y ángulos. Este cuadrilátero tiene dos pares de lados no paralelos, lo que hace imposible su división en partes iguales mediante un eje de simetría.

Mientras que el rectángulo, el cuadrado y el rombo tienen ejes de simetría que les permiten dividirse en dos partes idénticas, el trapezoide y el trapecio escaleno no cuentan con dichos ejes debido a la asimetría de sus características geométricas.

Qué es un eje de simetría y cómo se identifica en un cuadrilátero

Un eje de simetría en geometría es una línea imaginaria que divide una figura en dos partes idénticas y simétricas entre sí. En el caso de un cuadrilátero, un eje de simetría puede ser una línea vertical, horizontal o diagonal que pasa por su centro, dividiendo al cuadrilátero en dos mitades que son especulares entre sí.

La identificación de los ejes de simetría en un cuadrilátero depende de sus propiedades geométricas y la disposición de sus lados y ángulos. Para determinar si un cuadrilátero tiene ejes de simetría, es necesario analizar sus características individuales.

Cuadrado: el único cuadrilátero con cuatro ejes de simetría

El cuadrado es un cuadrilátero especial, ya que posee cuatro ejes de simetría. Estos ejes se corresponden con las diagonales, tanto internas como externas, que conectan los vértices opuestos del cuadrado.

Al trazar una línea a lo largo de cualquiera de estas diagonales, se puede observar que el cuadrado se divide en dos mitades idénticas, tanto en términos de longitud como de orientación. Además, estos ejes de simetría se cruzan en el centro del cuadrado, lo que proporciona una simetría múltiple.

Rectángulo: cuadrilátero con dos ejes de simetría

En el caso del rectángulo, encontramos dos ejes de simetría. Estos ejes se encuentran en las líneas medianas de los lados opuestos del rectángulo.

Si trazamos una línea a lo largo de uno de estos ejes de simetría, veremos que el rectángulo se divide en dos mitades simétricas. Ambas mitades tendrán la misma longitud, pero su orientación será diferente.

Rombo: cuadrilátero con un eje de simetría

El rombo es otro tipo de cuadrilátero que presenta un eje de simetría. Este eje pasa por los vértices opuestos del rombo y se denomina eje de simetría principal.

Cuando trazamos una línea a lo largo de este eje de simetría, el rombo se divide en dos partes especulares. Estas partes son idénticas en cuanto a longitud y orientación.

Es importante destacar que estos ejes de simetría no solo dividen al cuadrilátero en dos partes, sino que también reflejan cada punto de una mitad a la otra. Esto significa que si dibujamos cualquier figura o patrón en una mitad del cuadrilátero, este se reflejará automáticamente en la otra mitad a través del eje de simetría correspondiente.

Ahora ya sabes qué es un eje de simetría y cómo se identifica en diferentes tipos de cuadriláteros. Sin embargo, existe un cuadrilátero particular que desafía los conceptos tradicionales de simetría. Descubre a continuación el cuadrilátero que no tiene ejes de simetría.

Cómo puedo desafiar mis conocimientos en geometría con los cuadriláteros sin ejes de simetría

Si eres un amante de la geometría y te gusta poner a prueba tus conocimientos, seguramente estás buscando nuevos desafíos. En este artículo te proponemos descubrir qué cuadrilátero no tiene ejes de simetría y cómo puedes poner a prueba tus habilidades en geometría con ellos.

¿Qué es un eje de simetría en un cuadrilátero?

Antes de adentrarnos en el tema principal, es importante entender qué es un eje de simetría en un cuadrilátero. Un eje de simetría es una línea imaginaria que divide al cuadrilátero en dos partes iguales, reflejadas una sobre la otra. Es decir, si doblamos el cuadrilátero a lo largo del eje de simetría, las dos partes coincidirían perfectamente.

Cuadriláteros con ejes de simetría

Existen varios tipos de cuadriláteros que tienen ejes de simetría. Algunos ejemplos son el cuadrado, el rectángulo, el rombo y el trapecio isósceles. Estos cuadriláteros tienen características particulares que los hacen tener uno o más ejes de simetría.

• El cuadrado es un cuadrilátero con cuatro lados iguales y cuatro ángulos rectos. Tiene cuatro ejes de simetría, uno para cada lado.
• El rectángulo es un cuadrilátero con cuatro ángulos rectos, pero sus lados opuestos no son necesariamente iguales. Tiene dos ejes de simetría, uno vertical y otro horizontal que coinciden en su punto medio.
• El rombo es un cuadrilátero con sus cuatro lados iguales, pero sus ángulos internos no son necesariamente rectos. Tiene dos ejes de simetría, uno que pasa por los vértices opuestos y otro que pasa por los puntos medios de los lados.
• El trapecio isósceles es un cuadrilátero con dos lados paralelos y dos lados no paralelos. Tiene un eje de simetría que es la línea que conecta los puntos medios de los lados no paralelos.

Cuadriláteros sin ejes de simetría

Ahora llegamos al punto principal de este artículo: los cuadriláteros que no tienen ejes de simetría. Estos cuadriláteros son aquellos en los que no podemos encontrar ninguna línea que divida al cuadrilátero en dos partes iguales mediante reflexión. Aunque parezca sorprendente, existen varios cuadriláteros sin ejes de simetría.

• El romboide es un cuadrilátero con sus lados opuestos paralelos pero no necesariamente iguales. No tiene ejes de simetría.
• El trapezoide o trapecio no isósceles es un cuadrilátero con dos lados paralelos. No tiene ejes de simetría.
• El cuadrilátero irregular es aquel que no cumple con ninguna de las características de los cuadriláteros mencionados anteriormente. Tampoco tiene ejes de simetría.

Estos cuadriláteros sin ejes de simetría pueden ser una forma interesante de desafiar tus conocimientos en geometría. Al no contar con ejes de simetría, su estudio requiere de un análisis más completo y detallado, explorando sus diferentes propiedades y características geométricas.

Poniendo a prueba tus conocimientos

Ahora que ya sabes qué cuadriláteros no tienen ejes de simetría, llega el momento de poner a prueba tus conocimientos geométricos. Te proponemos algunos desafíos:

1. Crea un romboide con lados de longitudes específicas y comprueba si tiene algún eje de simetría. ¿Qué propiedades geométricas puedes identificar en este caso?
2. Dibuja un trapezoide no isósceles y analiza si tiene ejes de simetría. ¿Cuántos ángulos rectos o de 90 grados puede tener? ¿Qué otras características puedes encontrar en este tipo de cuadrilátero?
3. Explora las diferentes formas y propiedades de un cuadrilátero irregular. Sin ejes de simetría, ¿qué condiciones deben cumplirse para que sea un cuadrilátero válido? ¿Puedes dibujar un cuadrilátero irregular que tenga lados paralelos?

Recuerda que la clave para poner a prueba tus conocimientos en geometría es la observación y el análisis detallado de las propiedades geométricas de cada figura. A medida que te enfrentes a nuevos desafíos, estarás fortaleciendo tus habilidades y comprensión de los conceptos geométricos.

Así que atrévete a descubrir qué cuadrilátero no tiene ejes de simetría y desafía tus conocimientos en geometría. ¡Diviértete explorando el fascinante mundo de las figuras geométricas!

Existen casos especiales en los cuales un cuadrilátero puede tener más de un eje de simetría

En geometría, la simetría juega un papel fundamental en el estudio de las figuras y su estructura. Un ejemplo claro de simetría son los ejes de simetría, líneas imaginarias que dividen una figura en dos partes iguales y que reflejan perfectamente una sección en la otra.

Sin embargo, existen casos especiales en los cuales un cuadrilátero puede desafiar nuestros conocimientos sobre simetría. Estos cuadriláteros poseen características únicas que los distinguen del resto y no cuentan con ningún eje de simetría.

Cuadrilátero asimétrico: el caso inusual

El cuadrilátero asimétrico es aquel que no presenta ningún eje de simetría. A diferencia de otros cuadriláteros como el rectángulo, el cuadrado o el rombo, que sí poseen ejes de simetría, el cuadrilátero asimétrico no tiene ninguno de ellos.

Esta ausencia de ejes de simetría hace que el cuadrilátero asimétrico sea una figura única y desafiante desde el punto de vista geométrico. Su falta de simetría implica que no se puede dividir en dos partes iguales por ninguna línea.

Además, esta falta de ejes de simetría también nos indica que las diagonales de un cuadrilátero asimétrico no se cortan en un punto central como ocurre en otros cuadriláteros regulares. En cambio, las diagonales pueden tener longitudes diferentes y se intersectan en diferentes puntos.

Diferencias con otros cuadriláteros regulares

Una vez entendido el concepto de un cuadrilátero asimétrico, es importante conocer las diferencias que tiene con otros cuadriláteros regulares que sí presentan ejes de simetría.

Por ejemplo, en el caso de un cuadrado, podemos encontrar cuatro ejes de simetría: dos ejes horizontales y dos verticales. Estos ejes dividen al cuadrado en cuatro partes iguales y se reflejan perfectamente en las otras secciones.

En el caso de un rectángulo, encontramos también dos ejes de simetría: uno vertical y otro horizontal. Estos ejes permiten dividir al rectángulo en dos partes iguales a lo largo y ancho de la figura.

Finalmente, el rombo tiene dos ejes de simetría diagonales. Estos ejes de simetría cortan al rombo en sus ángulos y permiten dividirlo en dos partes iguales en forma de triángulos.

Los cuadriláteros asimétricos son una rareza en el estudio de la geometría. Su falta de ejes de simetría los convierte en figuras únicas y desafiantes para aquellos que buscan profundizar en sus conocimientos geométricos. A medida que exploramos el fascinante mundo de la geometría, es importante tener en cuenta estos casos especiales que nos hacen reflexionar sobre la naturaleza y la diversidad de las formas.

Cuál es la importancia de los ejes de simetría en la geometría y el arte

Los ejes de simetría son una herramienta fundamental en la geometría y el arte. En la geometría, los ejes de simetría nos permiten analizar y describir las figuras geométricas en términos de su balance y estructura. En el arte, los ejes de simetría juegan un papel clave en el diseño y la composición visual.

Un objeto o figura geométrica se considera simétrico cuando puede ser dividido en dos partes iguales a lo largo de uno o más ejes de simetría. Estos ejes pueden ser horizontales, verticales o incluso diagonales. Los ejes de simetría nos ayudan a identificar patrones y propiedades de las figuras, y nos permiten entender mejor sus características y relaciones internas.

Por ejemplo, el cuadrado es una figura geométrica que cuenta con cuatro ejes de simetría: dos horizontales y dos verticales. Esto significa que podemos dividir el cuadrado en cuatro partes iguales a lo largo de estos ejes. Esta simetría nos brinda una sensación de equilibrio y estabilidad visual.

Sin embargo, no todos los cuadriláteros tienen ejes de simetría. Existen ciertos cuadriláteros que no poseen ningún eje de simetría. Uno de los ejemplos más conocidos es el trapecio. Un trapecio es un cuadrilátero que tiene solamente un par de lados paralelos, lo que hace imposible encontrar un eje de simetría.

La ausencia de ejes de simetría en el trapecio lo hace único y desafiante desde el punto de vista geométrico. Su asimetría le confiere una apariencia distinta y atractiva en comparación con otros cuadriláteros. Esto lo convierte en un elemento interesante tanto en la geometría como en el arte, ya que agrega dinamismo y diversidad visual a cualquier composición.

Los ejes de simetría desempeñan un papel crucial en la geometría y el arte. Nos permiten analizar las figuras geométricas, identificar patrones y propiedades, y crear composiciones visualmente equilibradas. Aunque muchos cuadriláteros tienen ejes de simetría, hay algunos que desafían esta norma, como el trapecio. La ausencia de ejes de simetría en el trapecio lo hace único y añade interés visual a cualquier contexto en el que se utilice. Así que, si alguna vez te encuentras frente a un cuadrilátero sin ejes de simetría, no dudes en explorar sus características únicas y disfrutar del desafío que representa para tus conocimientos en geometría.

Existe alguna relación entre los cuadriláteros sin ejes de simetría y otras figuras geométricas

Los cuadriláteros son figuras geométricas que poseen cuatro lados y cuatro ángulos. Dentro de esta clasificación, existen diferentes tipos de cuadriláteros, como el cuadrado, el rectángulo, el rombo, el trapecio y el parallelogramo, entre otros. Cada uno de estos cuadriláteros tiene características específicas, como sus ángulos internos y lados iguales o paralelos.

En el contexto de los cuadriláteros sin ejes de simetría, se refiere a aquellos cuadriláteros en los que no se puede encontrar una línea recta que los divida en dos partes idénticas al realizar un giro de 180 grados alrededor de ese eje. Esto implica que no existe ninguna simetría con respecto a un eje específico para estas figuras.

Origen de la falta de ejes de simetría

La falta de ejes de simetría en un cuadrilátero puede deberse a diferentes factores, como las longitudes de los lados y los ángulos internos de la figura. Para comprender mejor este concepto, debemos analizar las características de algunos cuadriláteros específicos.

El trapecio como ejemplo de cuadrilátero sin ejes de simetría

Un ejemplo común de cuadrilátero sin ejes de simetría es el trapecio. Este cuadrilátero tiene un par de lados paralelos, llamados bases, y dos pares de ángulos opuestos que suman 180 grados cada uno. Sin embargo, debido a la asimetría de sus lados no paralelos y ángulos internos, el trapecio no tiene ejes de simetría.

Por otro lado, podemos encontrar cuadriláteros como el rectángulo y el cuadrado que sí tienen ejes de simetría. Estas figuras poseen lados iguales y sus ángulos internos miden 90 grados, lo que les confiere una alta simetría.

Relación con otras figuras geométricas

En cuanto a la relación entre los cuadriláteros sin ejes de simetría y otras figuras geométricas, es importante destacar que no todos los cuadriláteros se pueden clasificar exclusivamente como tales. Algunos cuadriláteros, como el rombo y el parallelogramo, pueden tener o no ejes de simetría, dependiendo de las características específicas de cada figura.

Estas características incluyen la longitud y ángulos de los lados, la congruencia de sus diagonales y otras propiedades especiales. Por lo tanto, no se puede establecer una relación directa entre los cuadriláteros sin ejes de simetría y otras figuras geométricas, ya que cada cuadrilátero debe ser analizado individualmente para determinar si tiene o no ejes de simetría.

Desafía tus conocimientos en geometría

La geometría es una rama fascinante de las matemáticas que nos permite comprender y describir las formas y relaciones espaciales. El estudio de los cuadriláteros sin ejes de simetría es solo uno de los muchos desafíos que podemos encontrar en esta disciplina.

Si eres un apasionado de la geometría y deseas poner a prueba tus conocimientos, te invitamos a explorar más sobre los cuadriláteros sin ejes de simetría y sus propiedades. Puedes buscar ejemplos específicos de estos cuadriláteros, investigar sobre las características de otras figuras geométricas o resolver problemas y ejercicios relacionados con este tema.

Recuerda que desafiar tus conocimientos en geometría no solo te permitirá aprender más sobre esta fascinante rama de las matemáticas, sino también desarrollar habilidades de razonamiento lógico y visualización espacial. ¡Atrévete a descubrir qué cuadrilátero no tiene ejes de simetría y amplía tus horizontes en la geometría!

Cuáles son algunos ejemplos de cuadriláteros sin ejes de simetría en la vida cotidiana

La simetría es un concepto fundamental en la geometría, ya que nos permite identificar formas y figuras que son iguales en ambos lados. Sin embargo, no todas las figuras geométricas tienen ejes de simetría y los cuadriláteros no son una excepción.

Un cuadrilátero es un polígono de cuatro lados, y puede tener diferentes características en cuanto a sus ángulos y lados. Algunos cuadriláteros comunes, como el cuadrado y el rectángulo, tienen ejes de simetría que los dividen en dos partes iguales.

Sin embargo, hay cuadriláteros que son asimétricos y no tienen ejes de simetría. Estas formas geométricas desafían nuestras intuiciones y conocimientos previos sobre la simetría. A continuación, veremos algunos ejemplos de cuadriláteros sin ejes de simetría que podemos encontrar en nuestra vida cotidiana.

1. Trapecio

El trapecio es un cuadrilátero con un par de lados paralelos y otro par de lados no paralelos. Aunque el trapecio puede parecer simétrico a simple vista, no tiene ejes de simetría. Podemos comprobarlo dibujando una línea que divida al trapecio en dos partes iguales: encontraremos que los lados no paralelos no se superponen. Esto significa que el trapecio no tiene ningún eje de simetría que lo atraviese.

2. Romboide

El romboide es otro ejemplo de cuadrilátero sin ejes de simetría. A diferencia del rombo, que sí tiene ejes de simetría debido a sus ángulos iguales, el romboide no cumple con esta propiedad. Para comprobarlo, podemos trazar una línea que divida al romboide en dos partes iguales: encontraremos que los lados no se superponen. Esto demuestra que el romboide carece de ejes de simetría.

3. Cuadrilátero irregular

Aparte de los cuadriláteros específicos mencionados anteriormente, los cuadriláteros irregulares también pueden carecer de ejes de simetría. Estos cuadriláteros tienen lados y ángulos desiguales, lo que los hace asimétricos en general. Su falta de simetría hace que no tengamos ninguna línea recta que pueda dividirlos en dos partes iguales.

Hay varios cuadriláteros que no tienen ejes de simetría. Ejemplos como el trapecio, el romboide y los cuadriláteros irregulares nos muestran cómo la geometría puede sorprendernos con formas asimétricas que desafían nuestras expectativas. Estos cuadriláteros sin ejes de simetría nos invitan a explorar y profundizar en los conceptos geométricos para comprender mejor las diferentes propiedades de las figuras.

Cómo la ausencia de ejes de simetría afecta las propiedades y características de un cuadrilátero

Cuando hablamos de geometría y de las propiedades de las figuras geométricas, los ejes de simetría juegan un papel fundamental. El concepto de simetría se refiere a la capacidad de una figura para reflejarse en un eje y coincidir consigo misma. Sin embargo, no todos los cuadriláteros tienen esta propiedad tan especial. Existe un tipo de cuadrilátero en particular que se destaca por la ausencia de ejes de simetría, desafiando así nuestros conocimientos y expectativas sobre las figuras geométricas.

Este cuadrilátero se conoce como "trompa de elefante" o "cuadrilátero asimétrico". Su peculiar nombre se debe precisamente a su falta de simetría y a su forma única y distintiva. A diferencia de los cuadriláteros más comunes, como el cuadrado o el rectángulo, este tipo de figura no posee ejes de simetría que le permitan reflejarse y mantener la congruencia entre sus partes.

A pesar de su aparente falta de simetría, el cuadrilátero sin ejes de simetría sigue siendo una figura fascinante desde el punto de vista matemático. Sus propiedades y características lo hacen digno de estudio y análisis detallado.

Propiedades del cuadrilátero sin ejes de simetría

• Ángulos internos: Aunque este cuadrilátero carece de ejes de simetría, los ángulos internos siguen manteniendo una serie de relaciones y propiedades. Por ejemplo, la suma de los ángulos internos de cualquier cuadrilátero siempre es igual a 360 grados. Esta regla se aplica también a la trompa de elefante.
• Lados: Los lados del cuadrilátero sin ejes de simetría pueden ser de diferentes longitudes. A diferencia de los cuadriláteros regulares, donde los lados opuestos son iguales, en este tipo de figura no existe una relación especial entre los lados.
• Diagonales: Las diagonales de este cuadrilátero son segmentos de línea que unen dos vértices no adyacentes. Estas diagonales pueden tener diferentes longitudes y no necesariamente se intersectan en un punto central, como sucede en el caso de los cuadriláteros con ejes de simetría.

A pesar de sus características inusuales, el cuadrilátero sin ejes de simetría ha sido objeto de estudio y análisis por parte de matemáticos y estudiantes de geometría. Su falta de simetría lo convierte en un desafío interesante para aquellos que buscan ampliar sus conocimientos y explorar nuevas formas y figuras geométricas.

Tip: Ponte a prueba y trata de dibujar un cuadrilátero sin ejes de simetría. ¡Seguro que te sorprenderás con los resultados!

Cuáles son las principales diferencias entre un cuadrilátero sin ejes de simetría y uno con ejes de simetría

En el maravilloso mundo de la geometría, los cuadriláteros son figuras que captan nuestra atención por sus formas y propiedades únicas. Uno de los conceptos más fascinantes relacionados con los cuadriláteros es la simetría. La simetría en una figura significa que se puede encontrar un eje de simetría que divide la figura en dos partes idénticas.

Pero, ¿qué sucede cuando hablamos de un cuadrilátero sin ejes de simetría? Aquí es donde las cosas se vuelven aún más interesantes y desafiantes. Un cuadrilátero sin ejes de simetría es aquel que no posee ninguna línea recta que lo divida en dos partes idénticas. Esto significa que no importa cómo intentemos dividirlo, nunca encontraremos dos partes que sean iguales entre sí.

Por otro lado, tenemos los cuadriláteros con ejes de simetría. Estos son aquellos que sí poseen al menos un eje de simetría, es decir, una línea recta que pasa a través de la figura y la divide en dos partes idénticas. Es importante mencionar que algunos cuadriláteros pueden tener más de un eje de simetría.

Ahora bien, ¿cuáles son las principales diferencias entre un cuadrilátero sin ejes de simetría y uno con ejes de simetría? Una diferencia clave radica en la simetría misma. Los cuadriláteros sin ejes de simetría pueden tener formas irregulares y asimétricas, lo que los hace visualmente más interesantes y desafiantes desde el punto de vista geométrico.

Por otro lado, los cuadriláteros con ejes de simetría suelen tener formas más regulares y balanceadas. Estas figuras pueden ser más fáciles de identificar y analizar, ya que cuentan con líneas rectas de referencia en las que podemos basarnos para comprender mejor su estructura geométrica.

Además, la presencia o ausencia de ejes de simetría también tiene implicaciones en las propiedades de los cuadriláteros. Por ejemplo, los cuadriláteros con ejes de simetría suelen tener ángulos diagonales iguales, lo que facilita el cálculo de diversas medidas y relaciones entre sus elementos. Por otro lado, los cuadriláteros sin ejes de simetría pueden presentar ángulos diagonales diferentes, lo que añade un nivel de complejidad adicional al estudio de estas figuras.

Los cuadriláteros sin ejes de simetría y los cuadriláteros con ejes de simetría son casos fascinantes dentro del mundo de la geometría. Mientras que los primeros nos desafían visualmente y nos invitan a explorar formas más irregulares, los segundos nos ofrecen estructuras más equilibradas y fáciles de analizar. Explorar estas diferencias nos permite ampliar nuestros conocimientos en geometría y apreciar la diversidad y belleza de las figuras geométricas.

Cuál es la importancia de comprender qué cuadrilátero no tiene ejes de simetría en la educación matemática

En el vasto mundo de la geometría, existe una amplia variedad de figuras y formas que se pueden explorar y analizar. Una de las propiedades más intrigantes de estas figuras es su simetría. La simetría es un concepto matemático fundamental que implica igualdad o correspondencia en forma, tamaño, posición y orientación alrededor de un punto, línea o plano.

En muchos casos, las figuras geométricas exhiben una o más líneas de simetría, también conocidas como ejes de simetría. Estos ejes dividen la figura en dos partes iguales, lo que significa que si doblamos la figura a lo largo del eje, ambas partes coincidirán exactamente.

Sin embargo, hay un cuadrilátero especial que rompe esta regla común. Se trata de un cuadrilátero que no tiene ningún eje de simetría, es decir, no se puede dividir en dos partes iguales mediante una línea recta que actúe como un eje de simetría. Este tipo de cuadrilátero desafía los conocimientos y la intuición geométrica, ya que no presenta ninguna forma de simetría evidente.

La importancia de comprender qué cuadrilátero no tiene ejes de simetría radica en varios aspectos en el campo de la educación matemática. En primer lugar, este conocimiento desafía a los estudiantes a pensar de manera más crítica y creativa, fomentando el desarrollo de habilidades de resolución de problemas y razonamiento deductivo.

Al enfrentarse a un cuadrilátero sin ejes de simetría, los estudiantes deben analizar cuidadosamente las propiedades y características de la figura para determinar si existe alguna forma inesperada de simetría. Esto implica examinar los ángulos, longitudes de los lados y disposición de las líneas en busca de patrones ocultos o asimetrías sutiles que podrían desafiar las expectativas.

Además, comprender qué cuadriláteros no tienen ejes de simetría amplía el conocimiento matemático de los estudiantes al presentarles situaciones problemáticas más desafiantes. Los cuadriláteros sin ejes de simetría son figuras más complejas y menos comunes en comparación con los cuadriláteros convencionales, lo que proporciona a los estudiantes una oportunidad de explorar nuevos territorios geométricos y desarrollar su capacidad para enfrentarse a problemas más difíciles.

• Por ejemplo, algunos ejemplos de cuadriláteros que no tienen ejes de simetría son:
1. El trapecio escaleno: un trapecio con sus lados no paralelos de distintas longitudes. Este tipo de trapecio rompe la simetría porque sus lados no se pueden dividir en partes iguales mediante ninguna línea recta.
2. El romboide: un paralelogramo con lados adyacentes de longitudes desiguales y ángulos no rectos. Aunque puede parecer simétrico debido a sus lados paralelos, no tiene ejes de simetría ya que sus lados no son iguales.

Comprender qué cuadrilátero no tiene ejes de simetría es una cuestión fascinante que desdibuja los límites tradicionales de la geometría. Este conocimiento desafía a los estudiantes a pensar más allá de las convenciones y expectativas establecidas, fomentando el desarrollo de habilidades matemáticas avanzadas y mejorando su capacidad para enfrentarse a problemas complejos. Explorar esta faceta singular de la geometría amplía el horizonte del conocimiento matemático y cultiva el pensamiento crítico y la creatividad en el aula.

Preguntas frecuentes (FAQ)

1. ¿Qué es un cuadrilátero?

Un cuadrilátero es una figura plana cerrada que tiene cuatro lados y cuatro ángulos.

2. ¿Cuántos ejes de simetría puede tener un cuadrilátero?

Un cuadrilátero puede tener hasta dos ejes de simetría.

3. ¿Cuál es el cuadrilátero que no tiene ejes de simetría?

El romboide no tiene ejes de simetría.

4. ¿Cuál es la diferencia entre un rombo y un romboide?

La principal diferencia entre un rombo y un romboide es que un rombo tiene todos sus lados iguales, mientras que un romboide tiene lados opuestos iguales pero no todos.

5. ¿Hay otros cuadriláteros que no tengan ejes de simetría?

Sí, además del romboide, el trapecio también es un cuadrilátero que no tiene ejes de simetría.