Descubre las increíbles 7 leyes de los exponentes: ¡domina las matemáticas con facilidad!
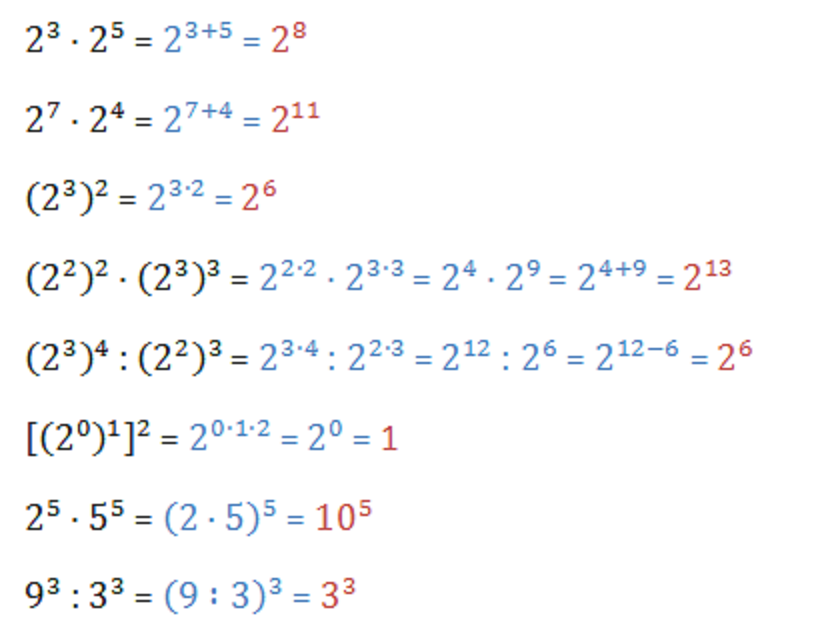
Las leyes de los exponentes son fundamentales en el estudio de las matemáticas. Estas reglas nos permiten simplificar y operar con expresiones algebraicas que involucran potencias. Al entender y dominar estas leyes, podemos resolver problemas más rápidamente y de manera más eficiente.
Te presentaré y explicaré las 7 leyes de los exponentes de manera clara y sencilla. Aprenderás cómo aplicar estas leyes a diferentes tipos de expresiones algebraicas, como multiplicación, división, potencias de potencias, entre otros. Al finalizar, estarás preparado para resolver problemas de exponentes con facilidad y confianza.
- Qué son los exponentes y cómo se utilizan en matemáticas
- Las propiedades fundamentales de los exponentes
- 1. Ley del producto
- 2. Ley de la potencia de una potencia
- 3. Ley de la potencia de cero
- 4. Ley del cociente
- 5. Ley de los exponentes negativos
- 6. Ley de la raíz n-ésima
- 7. Ley del producto de potencias de igual base
- Cuál es la ley del exponente cero y qué significa
- Cómo se aplican las leyes de los exponentes para simplificar expresiones algebraicas
- Cuáles son las propiedades de los exponentes negativos y cómo pueden ser utilizadas
- Qué es la ley del producto de exponentes y cómo se aplica en la multiplicación de potencias
- Cuál es la ley del cociente de exponentes y cómo se utiliza en la división de potencias
- Cómo se resuelven problemas que involucran exponentes con diferentes bases pero el mismo exponente
Qué son los exponentes y cómo se utilizan en matemáticas
Los exponentes son una herramienta poderosa en matemáticas que nos permite representar multiplicaciones repetidas de un número. Se utilizan para simplificar y agilizar cálculos que involucran operaciones con números grandes o pequeños.
En su forma más básica, un exponente consiste en dos elementos: la base y el exponente. La base es el número que se multiplicará por sí mismo, y el exponente representa cuántas veces se realizará la multiplicación.
Por ejemplo, si tenemos la expresión 23, la base es 2 y el exponente es 3. Esto significa que debemos multiplicar el número 2 consigo mismo 3 veces.
El resultado sería:
2 * 2 * 2 = 8
Como se puede observar, hemos simplificado una serie de multiplicaciones en una sola operación: 23 = 8.
Las propiedades fundamentales de los exponentes
Ahora que comprendemos qué son los exponentes y cómo se utilizan, es importante entender las leyes que rigen su manipulación. Estas leyes, también conocidas como propiedades de los exponentes, nos permiten realizar diferentes operaciones con ellos de manera eficiente.
1. Ley del producto
La ley del producto establece que cuando multiplicamos dos términos con la misma base, debemos sumar sus exponentes.
Por ejemplo, si tenemos la expresión 23 * 24, podemos aplicar esta propiedad para simplificarla. La base en ambos términos es 2, por lo que sumaremos los exponentes:
23 * 24 = 27
2. Ley de la potencia de una potencia
La ley de la potencia de una potencia nos indica que cuando tenemos un exponente elevado a otro exponente, debemos multiplicar los exponentes.
Por ejemplo, si tenemos la expresión (23)2, podemos aplicar esta propiedad para simplificarla. Multiplicaremos los exponentes 3 y 2:
(23)2 = 26
3. Ley de la potencia de cero
La ley de la potencia de cero establece que cualquier número elevado a la potencia de cero es igual a 1.
Por ejemplo, si tenemos la expresión 50, según esta ley, el resultado sería:
50 = 1
4. Ley del cociente
La ley del cociente establece que cuando dividimos dos términos con la misma base, debemos restar sus exponentes.
Por ejemplo, si tenemos la expresión 85 / 82, podemos aplicar esta propiedad para simplificarla. La base en ambos términos es 8, por lo que restaremos los exponentes:
85 / 82 = 83
5. Ley de los exponentes negativos
La ley de los exponentes negativos establece que cuando tenemos una base elevada a un exponente negativo, el resultado es igual a la inversa de la misma base elevada al exponente positivo.
Por ejemplo, si tenemos la expresión 4-3, podemos aplicar esta propiedad para simplificarla:
4-3 = 1 / 43 = 1 / 64
6. Ley de la raíz n-ésima
La ley de la raíz n-ésima establece que podemos representar una raíz n-ésima como una potencia con exponente fraccionario.
Por ejemplo, si tenemos la expresión √(16), podemos aplicar esta propiedad para simplificarla:
√(16) = 161/2 = 4
7. Ley del producto de potencias de igual base
La ley del producto de potencias de igual base establece que, cuando multiplicamos varias potencias con la misma base, debemos sumar los exponentes.
Por ejemplo, si tenemos la expresión (32) * (34) * (35), podemos aplicar esta propiedad para simplificarla. La base en todos los términos es 3, por lo que sumaremos los exponentes:
(32) * (34) * (35) = 311
Estas son solo algunas de las leyes fundamentales de los exponentes. Dominarlas te permitirá resolver problemas matemáticos con mayor facilidad y precisión.
Recuerda practicar y aplicar estas leyes en diferentes ejercicios para afianzar tu comprensión de los exponentes. ¡Sigue adelante y conviértete en un experto en matemáticas!
Cuál es la ley del exponente cero y qué significa
La ley del exponente cero es una de las siete leyes fundamentales que rigen los exponentes en matemáticas. Esta ley establece que cualquier número elevado a la potencia de cero siempre será igual a uno.
Por ejemplo, si tenemos el número 5 elevado a la potencia de cero:
50
El resultado sería igual a 1:
50 = 1
Esta propiedad es válida para cualquier número real diferente de cero o cualquier variable no nula elevada a la potencia de cero. La ley del exponente cero se basa en el principio básico de que cualquier número o cantidad multiplicada por uno sigue siendo igual a sí misma.
La importancia de la ley del exponente cero radica en su relación con otras propiedades y operaciones relacionadas con los exponentes. Por ejemplo, al combinar esta ley con la ley del producto de exponentes, podemos simplificar y resolver expresiones algebraicas más fácilmente. Además, también tiene aplicaciones prácticas en diversos campos como la física, la química y la economía.
Es importante tener en cuenta que la ley del exponente cero no es aplicable al caso especial de 0 elevado a la potencia de cero. En lugar de tener un valor definido, esta expresión es considerada indeterminada y puede dar lugar a diferentes resultados dependiendo del contexto y las reglas específicas utilizadas.
Cómo se aplican las leyes de los exponentes para simplificar expresiones algebraicas
Las leyes de los exponentes son fundamentales en el estudio del álgebra y su comprensión es clave para simplificar expresiones algebraicas de manera más eficiente. Estas leyes nos permiten operar con potencias de una manera más sencilla, reduciendo la complejidad de las ecuaciones y facilitando los cálculos.
Ley del producto de potencias de igual base
La primera ley de los exponentes establece que, cuando se multiplican dos potencias que tienen la misma base, se deben sumar los exponentes. Esto se puede representar matemáticamente de la siguiente manera:
a^m * a^n = a^(m + n)
Donde "a" es la base y "m" y "n" son los exponentes. Esta ley nos permite simplificar las expresiones algebraicas al combinar términos con la misma base y sumar sus exponentes correspondientes.
Ley del cociente de potencias de igual base
La segunda ley de los exponentes establece que, cuando se dividen dos potencias que tienen la misma base, se deben restar los exponentes. Matemáticamente, esta ley se expresa de la siguiente manera:
a^m / a^n = a^(m - n)
Al igual que en la ley del producto de potencias de igual base, esta ley nos permite simplificar las expresiones algebraicas al combinar términos con la misma base y restar sus exponentes correspondientes.
Ley de la potencia de potencia
La tercera ley de los exponentes establece que, cuando una potencia se encuentra elevada a otra potencia, se deben multiplicar los exponentes. Esta ley se representa matemáticamente de la siguiente manera:
(a^m)^n = a^(m * n)
Esta ley nos permite simplificar las expresiones algebraicas al realizar la operación de exponente sobre el exponente, obteniendo un nuevo exponente resultante.
Ley del producto de potencias de distinta base con el mismo exponente
La cuarta ley de los exponentes establece que, cuando se multiplica más de una potencia que tienen distintas bases pero el mismo exponente, se deben multiplicar las bases y mantener el exponente constante. Matemáticamente, esta ley se expresa de la siguiente manera:
a^m * b^m = (a * b)^m
Esta ley nos permite simplificar las expresiones algebraicas al combinar términos con distintas bases pero el mismo exponente, realizando la multiplicación entre las bases manteniendo el exponente constante.
Ley del cociente de potencias de distinta base con el mismo exponente
La quinta ley de los exponentes establece que, cuando se divide más de una potencia que tienen distintas bases pero el mismo exponente, se deben dividir las bases y mantener el exponente constante. Matemáticamente, esta ley se expresa de la siguiente manera:
a^m / b^m = (a / b)^m
De manera similar a la ley anterior, esta ley nos permite simplificar las expresiones algebraicas al combinar términos con distintas bases pero el mismo exponente, realizando la división entre las bases manteniendo el exponente constante.
Ley de potencia cero
La sexta ley de los exponentes establece que cualquier número diferente de cero elevado a la potencia cero es igual a uno. Esta ley se representa matemáticamente de la siguiente manera:
a^0 = 1
Es importante tener en cuenta que la base "a" debe ser diferente de cero en esta ley. Indica que cualquier número elevado a la potencia cero da como resultado uno.
Ley de potencia uno
La séptima y última ley de los exponentes establece que cualquier número elevado a la potencia uno es igual a sí mismo. Matemáticamente, se expresa de la siguiente manera:
a^1 = a
Esta ley nos indica que cualquier número elevado a la potencia uno se mantiene igual, sin cambios.
Las leyes de los exponentes son herramientas poderosas que nos permiten simplificar expresiones algebraicas y realizar cálculos más eficientemente. Con una comprensión sólida de estas leyes, podrás dominar las matemáticas y resolver problemas de manera más r rápida y precisa.
Cuáles son las propiedades de los exponentes negativos y cómo pueden ser utilizadas
Las propiedades de los exponentes negativos son fundamentales en el estudio de las matemáticas. Aunque puede parecer un tema complicado al principio, entender y aplicar estas propiedades te facilitará enormemente el cálculo con números elevados a potencias negativas.
Ley del exponente negativo
La ley del exponente negativo establece que cualquier número o variable elevada a una potencia negativa es igual a la inversa de dicho número o variable elevado a la potencia positiva correspondiente. En términos más sencillos, si tenemos un número 'a' elevado a la potencia '-n', donde 'a' es distinto de cero, entonces:
a-n = 1 / (an)
Por ejemplo, si tenemos 2-3, para obtener el resultado podemos aplicar la ley del exponente negativo de la siguiente manera:
2-3 = 1 / (23) = 1 / 8 = 0.125
Como puedes ver, el resultado es 0.125, que es la fracción 1/8 expresada como decimal.
Ejemplos de aplicación de la ley del exponente negativo
Veamos algunos ejemplos más para comprender mejor cómo se aplica esta propiedad:
5-2 = 1 / (52) = 1 / 25 = 0.04x-4 = 1 / (x4)(-3)-3 = 1 / ((-3)3)
En los casos anteriores, el proceso consiste en encontrar la inversa del número o variable elevada a la potencia positiva correspondiente.
Propiedad de la potencia de una fracción
Otra propiedad importante relacionada con los exponentes negativos es la propiedad de la potencia de una fracción. Si tenemos una fracción 'a/b' y la elevamos a una potencia '-n', podemos reescribirlo como:
(a/b)-n = (b/a)n
En este caso, simplemente intercambiamos el numerador y el denominador y cambiamos el signo del exponente.
Ejemplo de aplicación de la propiedad de la potencia de una fracción
Veamos un ejemplo para entender mejor cómo se utiliza esta propiedad:
(2/3)-2 = (3/2)2 = 9/4
En este caso, primero invertimos la fracción original, obteniendo '3/2', y luego elevamos esta nueva fracción al cuadrado, lo que nos da como resultado '9/4'.
Estas propiedades son esenciales para realizar cálculos más rápidos y eficientes con números elevados a potencias negativas. A medida que te familiarices con ellas, podrás resolver ecuaciones y problemas matemáticos de manera más sencilla.
Qué es la ley del producto de exponentes y cómo se aplica en la multiplicación de potencias
La ley del producto de exponentes es una de las leyes fundamentales en el estudio de las potencias. Esta ley nos permite simplificar la multiplicación de potencias con la misma base, al sumar los exponentes. En otras palabras, cuando tenemos dos potencias con la misma base y las multiplicamos, podemos combinar los exponentes para obtener un único exponente.
La expresión general de esta ley es:
am * an = am+n
Donde "a" representa la base de las potencias, y "m" y "n" son los exponentes correspondientes. Al aplicar la ley del producto de exponentes, simplemente sumamos los exponentes y dejamos la misma base. Esto nos permite simplificar la multiplicación y obtener una única potencia.
Veamos un ejemplo:
23 * 24 = 27
En este caso, tenemos dos potencias con la misma base (2) y las multiplicamos. Aplicando la ley del producto de exponentes, sumamos los exponentes (3+4) y obtenemos 7. Por lo tanto, la expresión se simplifica a 27.
Es importante destacar que esta ley solo se aplica cuando las bases de las potencias son iguales. Si las bases son diferentes, no podemos simplificar la multiplicación utilizando la ley del producto de exponentes.
Cuando hay múltiples términos en la multiplicación
Además de poder aplicar la ley del producto de exponentes a dos términos, también podemos utilizarla cuando tenemos más de dos términos en la multiplicación. Para ello, simplemente debemos sumar todos los exponentes correspondientes a la misma base.
Veamos un ejemplo:
32 * 33 * 34 = 39
En este caso, tenemos tres términos con la misma base (3) y los multiplicamos. Aplicando la ley del producto de exponentes, sumamos los exponentes (2+3+4) y obtenemos 9. Por lo tanto, la expresión se simplifica a 39.
De esta manera, la ley del producto de exponentes nos permite simplificar la multiplicación de potencias con la misma base, facilitando así los cálculos y proporcionando una herramienta fundamental en el estudio de las matemáticas.
Cuál es la ley del cociente de exponentes y cómo se utiliza en la división de potencias
La ley del cociente de exponentes es una de las siete leyes fundamentales que rigen el álgebra de exponentes. Esta ley nos permite simplificar la división de potencias y facilita enormemente los cálculos matemáticos.
La fórmula básica de la ley del cociente de exponentes establece que cuando dividimos dos bases iguales elevadas a diferentes potencias, podemos restar los exponentes para obtener un único exponente. En otras palabras:
am ÷ an = am - n
Veamos un ejemplo para entender mejor cómo funciona esta ley. Supongamos que tenemos la expresión 105 ÷ 102. Según la ley del cociente de exponentes, podemos restar los exponentes (5 - 2) y obtenemos 103.
Esta ley puede resultar especialmente útil cuando trabajamos con fracciones algebraicas o cuando necesitamos simplificar problemas más complejos. Por ejemplo, si tenemos la expresión (x4y3)2 ÷ (x2y2), podemos aplicar la ley del cociente de exponentes tanto en las bases x como en las bases y, restándolos para simplificar la expresión.
No obstante, es importante recordar que la ley del cociente de exponentes solo se aplica cuando las bases son iguales. Si las bases no son iguales, debemos utilizar otras leyes de los exponentes para resolver la expresión.
La ley del cociente de exponentes nos permite simplificar la división de potencias al restar los exponentes de las bases iguales. Esta ley es especialmente útil en álgebra y nos permite resolver problemas más rápido y de manera más eficiente. Recuerda que es fundamental comprender y dominar las siete leyes de los exponentes para poder desenvolvernos con facilidad en el mundo de las matemáticas.
Cómo se resuelven problemas que involucran exponentes con diferentes bases pero el mismo exponente
Resolver problemas que involucran exponentes con diferentes bases pero el mismo exponente puede parecer complicado al principio, pero con un poco de práctica y comprensión de las leyes de los exponentes, podrás dominar esta área de las matemáticas sin dificultad. En esta sección, exploraremos cómo resolver este tipo de problemas paso a paso.
Paso 1: Identificar las bases y el exponente
El primer paso para resolver problemas con exponentes es identificar las bases y el exponente que se encuentran en la expresión. Por ejemplo, consideremos el siguiente problema:
2^3 * 3^3
En este caso, la base 2 tiene un exponente de 3 y la base 3 también tiene un exponente de 3.
Paso 2: Aplicar la ley de los exponentes con el mismo exponente
Ahora que hemos identificado las bases y el exponente, podemos aplicar la ley de los exponentes que dice "cuando tienes exponentes con la misma base, puedes multiplicar las bases y mantener el mismo exponente". En nuestro ejemplo, esto significa que podemos multiplicar las bases 2 y 3 juntas y mantener el exponente 3:
(2 * 3)^3
Esto se simplifica a:
6^3
Paso 3: Resolver la expresión simplificada
Una vez que hemos simplificado la expresión, el siguiente paso es resolverla. En este caso, tenemos una base de 6 con un exponente de 3. Para resolverlo, simplemente multiplicamos la base por sí misma tantas veces como indica el exponente:
6 * 6 * 6
Esto se reduce a:
216
Por lo tanto, la solución a nuestra expresión original es 216.
Recuerda practicar mucho para familiarizarte con este tipo de problemas y las leyes de los exponentes. Cuanto más practiques, más fácil te resultará resolverlos. ¡No temas a los exponentes, son solo otra herramienta matemática que puedes dominar!
Los exponentes son una forma de representar la multiplicación repetida de un número por sí mismo. Por ejemplo, 2^3 significa 2 multiplicado por sí mismo tres veces: 2x2x2 = 8.
La regla básica de los exponentes establece que cuando tienes una base elevada a una potencia y esa potencia se multiplica por otra potencia, debes sumar los exponentes. Por ejemplo, (3^2)^3 = 3^(2x3) = 3^6.
Para multiplicar números con exponentes, debes mantener la misma base y sumar los exponentes. Por ejemplo, 4^2 x 4^3 = 4^(2+3) = 4^5.
Para dividir números con exponentes, debes mantener la misma base y restar los exponentes. Por ejemplo, 10^4 ÷ 10^2 = 10^(4-2) = 10^2.
Cuando tienes un número negativo como exponente, es equivalente a dividir 1 entre el número con el exponente positivo. Por ejemplo, 2^-3 = 1/2^3 = 1/8.
Entradas relacionadas