¡Descubre el amplio rango de la función seno y sorpréndete con sus infinitas posibilidades!

La función seno es una de las funciones más fundamentales en matemáticas y juega un papel crucial en muchas áreas como la física, la geometría y la ingeniería. El seno, junto con el coseno y la tangente, es una de las funciones trigonométricas más utilizadas.

En este artículo exploraremos el amplio rango de la función seno, desde su definición básica hasta sus diversas aplicaciones en el mundo real. También examinaremos los patrones y propiedades interesantes de esta función, como los períodos, amplitudes, frecuencias y otras características que la hacen tan fascinante.

Qué es la función seno y cómo se representa matemáticamente

La función seno es una de las funciones trigonométricas más importantes en matemáticas. Se utiliza ampliamente en diversos campos como la física, la ingeniería y la música. Esta función representa la relación entre los ángulos de un triángulo rectángulo y las longitudes de sus lados. El seno de un ángulo se define como la longitud del cateto opuesto dividido por la hipotenusa.

Matemáticamente, la función seno se representa con la letra "sin" seguida de un paréntesis que contiene el valor del ángulo en radianes o grados, según la convención utilizada. Por ejemplo, si queremos calcular el seno de un ángulo de 45 grados, escribimos sin(45°) o sin(pi/4) si lo expresamos en radianes.

La función seno tiene un rango infinito, es decir, puede tomar cualquier valor real entre -1 y 1. La amplitud de este rango nos muestra la propiedad periódica de la función seno. Esto significa que la función se repite cada cierto intervalo de tiempo o espacio.

Propiedades de la función seno

• Simetría: La función seno tiene simetría impar, lo que significa que sin(-x) = -sin(x). Esto implica que el seno de un ángulo negativo es igual a menos el seno del mismo ángulo positivo.
• Periodicidad: La función seno es periódica con un período de 2π (radianes) o 360° (grados). Esto significa que el valor del seno se repite cada 2π o 360°.
• Amplitud: La amplitud de la función seno es 1, lo que significa que su rango es entre -1 y 1. Esto implica que el valor absoluto del seno de cualquier ángulo está siempre acotado entre 0 y 1.
• Crecimiento: La función seno crece y decrece de forma continua en su rango . Al inicio, el seno aumenta rápidamente hasta alcanzar su máximo en π/2 radianes o 90°, luego disminuye nuevamente hasta alcanzar un mínimo en 3π/2 radianes o 270°, antes de volver a aumentar.

La función seno permite relacionar los ángulos de un triángulo rectángulo con las longitudes de sus lados. Posee propiedades interesantes como simetría impar, periodicidad y un rango infinito. Su amplio rango y su comportamiento periódico hacen que la función seno sea una herramienta fundamental en matemáticas y otras disciplinas.

Cuál es el rango de la función seno y por qué es tan amplio

Cuando hablamos de la función seno, nos referimos a una de las funciones trigonométricas fundamentales en matemáticas. Esta función sinusoidal ha sido estudiada y utilizada desde hace siglos, debido a sus múltiples aplicaciones en campos como la física, la ingeniería y la música.

El rango de la función seno es infinito, lo que significa que los valores que puede asumir son innumerables. Esto se debe a su naturaleza periódica, que se repite de forma constante a lo largo del eje de las coordenadas.

La función seno está definida para todos los números reales, lo que implica que su rango también incluye todos los números reales. Sin embargo, el valor máximo que puede alcanzar es 1 y el valor mínimo es -1. Estos extremos se encuentran en los puntos donde la función atraviesa el eje horizontal, es decir, los puntos donde el ángulo medido en radianes es un múltiplo entero de π. Estos puntos son conocidos como los "ceros" de la función.

Es importante destacar que, a pesar de su rango infinito, la función seno es limitada por sus propias propiedades matemáticas. Por ejemplo, su amplitud determina cuánto se aleja la función de su valor promedio. Cuanto mayor sea la amplitud, más varía la función y más amplio será su rango.

Aplicaciones del amplio rango de la función seno

• Física: La función seno se utiliza para describir el movimiento oscilatorio y ondulatorio de muchos fenómenos físicos, como las ondas sonoras, las ondas electromagnéticas y las oscilaciones de un péndulo. Su amplio rango permite representar con precisión estas vibraciones en el tiempo y el espacio.
• Ingeniería: En campos como la electrónica, la acústica y la comunicación, la función seno se utiliza para modelar y analizar señales periódicas. El rango infinito de la función seno es crucial para poder transmitir información de manera eficiente y precisa.
• Música: La función seno también juega un papel fundamental en la teoría musical. Las notas musicales se generan mediante ondas sonoras que siguen patrones sinusoidales. El amplio rango de la función seno permite crear una gran variedad de tonos y frecuencias en la música.

El rango de la función seno es tan amplio como infinito. Su naturaleza periódica y su capacidad para describir movimientos oscilatorios hacen que sea una herramienta indispensable en diversas disciplinas científicas y prácticas. Así que continúa explorando las infinitas posibilidades que ofrece esta fascinante función trigonométrica y sorpréndete con sus aplicaciones en el mundo real.

Cómo se puede utilizar la función seno en problemas de trigonometría

La función seno es una de las funciones trigonométricas más importantes y se utiliza ampliamente en problemas de trigonometría. Es una función periódica que tiene infinitas posibilidades y ofrece una gran cantidad de información sobre las relaciones entre los ángulos y las longitudes de los lados en un triángulo.

La forma más básica de utilizar la función seno es calcular el valor del seno de un ángulo dado en un triángulo rectángulo. En un triángulo rectángulo, el seno de un ángulo agudo se define como la relación entre la longitud del cateto opuesto al ángulo y la hipotenusa.

Para calcular el valor del seno de un ángulo, simplemente dividimos la longitud del cateto opuesto a ese ángulo por la longitud de la hipotenusa. Esto nos da un número decimal que representa la relación entre esas dos longitudes.

Por ejemplo, si tenemos un triángulo rectángulo con un ángulo de 30 grados y el cateto opuesto mide 8 unidades mientras que la hipotenusa mide 10 unidades, entonces podemos calcular el seno de ese ángulo dividiendo 8 por 10, lo que nos da 0.8. Esto significa que el seno de 30 grados es igual a 0.8.

Además de su uso en problemas relacionados con triángulos rectángulos, la función seno también se utiliza en otros contextos de trigonometría. Se puede encontrar el valor del seno de cualquier ángulo utilizando fórmulas específicas o tablas trigonométricas. Estas fórmulas o tablas nos proporcionan directamente el valor del seno de cualquier ángulo dado, lo que puede ser útil en una variedad de situaciones.

Otra forma común de utilizar la función seno es en problemas de modelado y simulación. En estos casos, se utiliza el seno para representar patrones periódicos, como las oscilaciones de un péndulo o las fluctuaciones de corriente alterna en un circuito eléctrico. El uso del seno en modelos matemáticos nos permite predecir y comprender el comportamiento de estos fenómenos con mayor precisión.

La función seno es una herramienta fundamental en trigonometría y tiene una amplia gama de aplicaciones. Se utiliza para calcular relaciones entre los ángulos y las longitudes de los lados en triángulos rectángulos, así como para modelar y simular fenómenos periódicos en diferentes contextos. Comprender cómo utilizar la función seno correctamente es esencial para resolver problemas de trigonometría de manera efectiva.

Qué relación tiene la función seno con el ciclo de las mareas

La función seno es una de las funciones trigonométricas más conocidas y tiene aplicaciones en una variedad de campos. Una de las relaciones interesantes que tiene el seno es con el ciclo de las mareas.

El ciclo de las mareas se refiere al patrón regular de las subidas y bajadas del nivel del mar que ocurren a lo largo de las costas. Estas variaciones son causadas principalmente por la atracción gravitacional de la Luna y, en menor medida, del Sol.

La función seno se utiliza para modelar estas fluctuaciones en el nivel del mar a lo largo del tiempo. La forma de onda sinusoidal creada por la función seno se ajusta muy bien a los patrones observados en las mareas.

Al estudiar el ciclo de las mareas, los científicos pueden analizar las amplitudes y frecuencias de las ondas sinusoidales generadas por el seno. Esto les permite predecir con precisión las alturas de las mareas en diferentes momentos del día o en diferentes días del año.

Además de su utilidad práctica en la predicción de las mareas, la relación entre la función seno y el ciclo de las mareas también es fascinante desde un punto de vista matemático. La manera en que el seno puede describir con precisión estos fenómenos naturales demuestra el poder y la versatilidad de las funciones trigonométricas.

La función seno está estrechamente relacionada con el ciclo de las mareas y se utiliza para modelar las variaciones en el nivel del mar a lo largo del tiempo. Esta relación entre la función matemática y un fenómeno natural demuestra tanto la aplicabilidad de las funciones trigonométricas como la fascinante conexión entre las matemáticas y el mundo real.

Cuáles son las aplicaciones prácticas de la función seno en el mundo real

La función seno es una de las funciones trigonométricas más importantes y ampliamente utilizadas en el mundo real. Sus aplicaciones prácticas son numerosas y se encuentran en diversos campos de estudio y áreas profesionales.

Física

En física, la función seno es esencial para describir fenómenos oscilatorios, como el movimiento ondulatorio, las vibraciones y las ondas sonoras. Por ejemplo, en el estudio de las ondas electromagnéticas, la función seno se utiliza para representar la amplitud de la onda en función del tiempo o la posición.

Además, en mecánica, la función seno se emplea para modelar el movimiento armónico simple, que es un tipo de movimiento vibratorio caracterizado por una trayectoria sinusoidal.

Ingeniería

En ingeniería, la función seno se utiliza ampliamente en el diseño y análisis de circuitos eléctricos y electrónicos. En estos casos, la función seno se emplea para describir las señales periódicas que se generan en los sistemas eléctricos y electrónicos, como las señales de corriente alterna.

También en ingeniería, la función seno es fundamental en el análisis de estructuras y materiales sometidos a fuerzas oscilatorias, como puentes colgantes, edificios ante terremotos o vibraciones en aviones y automóviles. La función seno ayuda a determinar la respuesta de estas estructuras ante dichas fuerzas y predecir su comportamiento.

Matemáticas

En matemáticas, la función seno tiene una amplia gama de aplicaciones. En trigonometría, la función seno es un elemento fundamental para calcular las relaciones entre los ángulos y los lados en triángulos rectángulos.

Además, la función seno se utiliza en otras ramas de las matemáticas como el cálculo, donde ayuda a modelar fenómenos de cambio continuo como el crecimiento exponencial o la propagación de enfermedades. También es útil en la resolución de ecuaciones diferenciales, que son herramientas fundamentales en muchas disciplinas científicas y técnicas.

Computación y gráficos

La función seno también desempeña un papel importante en la computación y los gráficos por computadora. Por ejemplo, en programación, se usa para generar efectos de animación suaves y fluidos, así como para la interpolación y el mapeo de valores.

En gráficos por computadora, la función seno se emplea para crear formas y curvas suaves, como en el modelado y renderizado de objetos tridimensionales. También se utiliza en algoritmos de simulación física, como en juegos y películas animadas.

La función seno es una herramienta poderosa y versátil con múltiples aplicaciones prácticas en diferentes campos. Su capacidad para representar fenómenos oscilatorios y su relación con los triángulos y el cambio continuo la convierten en una función fundamental en la ciencia, la tecnología y las matemáticas.

Cómo se puede graficar la función seno y qué información nos proporciona su gráfica

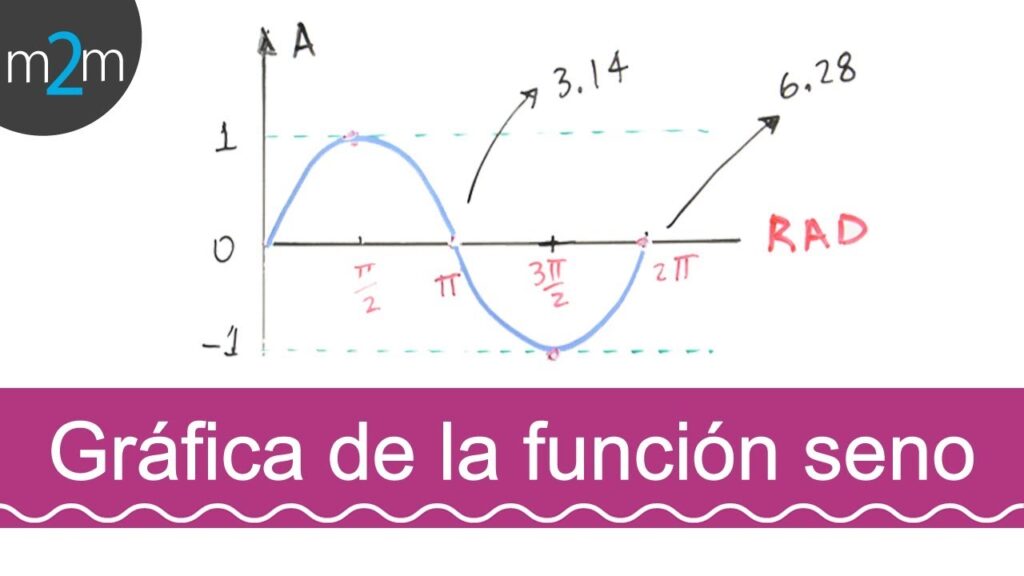
La función seno es una de las funciones trigonométricas más conocidas y utilizadas en matemáticas. Su grafica, también conocida como una onda sinusoidal, no solo tiene un amplio rango, sino que también nos proporciona una gran cantidad de información útil.

Para poder graficar la función seno, necesitamos saber cómo varía su valor en relación con el ángulo. En matemáticas, el ángulo se mide en radianes, por lo que el dominio de la función seno es el conjunto de todos los números reales. El rango de la función seno está acotado entre -1 y 1, lo que significa que el valor de seno(x) siempre estará entre estos dos límites.

La gráfica de la función seno tiene ciertas características distintivas. Es una curva periódica, lo que significa que se repite después de cierto intervalo de longitud. La longitud de esta repetición es 2π radianes o 360 grados, lo que indica que la función seno tiene un período de 2π.

Además, la gráfica de la función seno es simétrica con respecto al eje vertical, es decir, posee una simetría par. Esto significa que para cada valor positivo de x, también tendremos un valor negativo correspondiente en el mismo punto de la curva. Esta simetría es evidente si observamos que sin(-x) = -sen(x).

Otra propiedad interesante de la gráfica del seno es que pasa por el origen de coordenadas, es decir, sen(0) = 0. Esto nos ayuda a establecer puntos de referencia en la gráfica y determinar diferentes características.

Una vez que hemos comprendido estas características básicas de la gráfica del seno, podemos utilizar esta información para interpretar y analizar otras funciones o fenómenos que siguen un patrón similar. Por ejemplo, muchas ondas sonoras y electromagnéticas se pueden modelar utilizando la función seno.

Aplicaciones prácticas del seno y su representación gráfica

La función seno y su gráfica tienen numerosas aplicaciones prácticas en diversas áreas. Una de las aplicaciones más comunes es en física, donde se utiliza para describir movimientos oscilatorios como el péndulo, las ondas sonoras y las ondas electromagnéticas.

En ingeniería, la función seno y su gráfica también son fundamentales en el análisis de circuitos eléctricos y sistemas mecánicos. Las señales periódicas, como las corrientes alternas, se representan utilizando la función seno. Esta representación es esencial para entender cómo funcionan los sistemas y cómo se comportan en diferentes situaciones.

Además, la función seno es utilizada en matemáticas aplicadas y cálculo para modelar y resolver problemas relacionados con fenómenos periódicos. Al comprender y analizar la gráfica del seno, podemos obtener información importante como el valor máximo y mínimo, el período, la frecuencia y la amplitud de una función periódica.

La función seno y su gráfica nos proporcionan una amplia gama de posibilidades para entender y describir fenómenos periódicos en diversas áreas del conocimiento. Su análisis y aplicaciones prácticas son fundamentales para el desarrollo de disciplinas como la física, la ingeniería y las matemáticas aplicadas.

Existen otras funciones relacionadas con el seno que también tienen un rango amplio

Además de la función seno, en matemáticas existen otras funciones relacionadas que también tienen un rango amplio y ofrecen infinitas posibilidades para su estudio y aplicación en distintas áreas.

Una de las funciones más conocidas es la función coseno. Al igual que el seno, el coseno es una función periódica que oscila entre -1 y 1. La principal diferencia entre ambas funciones radica en la fase inicial de sus respectivas gráficas. Mientras que el seno inicia en el punto máximo, el coseno lo hace en el punto mínimo.

Otra función importante es la tangente. Esta función está definida como la razón entre el seno y el coseno de un ángulo dado. A diferencia del seno y el coseno, la tangente puede tomar cualquier valor real, lo que le otorga un rango ilimitado.

La cotangente es otra función relacionada con el seno y el coseno. Esta se define como la inversa de la tangente y también tiene un rango ilimitado. La gráfica de la cotangente presenta puntos de discontinuidad en los ángulos donde el coseno es igual a cero, ya que en esos casos la tangente no está definida.

Existen otras funciones trigonométricas menos conocidas pero igualmente importantes, como la secante y la cosecante. La secante es el recíproco del coseno, mientras que la cosecante es el recíproco del seno. Ambas funciones tienen un rango ilimitado y presentan puntos de discontinuidad en aquellos ángulos donde el seno o el coseno son iguales a cero.

Es fascinante explorar todas estas funciones y descubrir cómo se relacionan entre sí. Sus propiedades y aplicación en diversos campos de la ciencia, la ingeniería y la tecnología son fundamentales para entender el mundo que nos rodea.

Qué curiosidades o propiedades interesantes tiene la función seno

El comportamiento periódico del seno

Una de las propiedades más destacadas de la función seno es su comportamiento periódico. Es decir, se repite una y otra vez a lo largo de la recta numérica. Esto se debe a que el seno está definido en términos de un círculo unitario, donde el valor del seno de un ángulo depende de la posición de un punto en dicho círculo.

Esta periodicidad se puede observar fácilmente al graficar la función seno. Podemos ver cómo los valores de la función suben y bajan repetidamente a medida que avanzamos a lo largo del eje x. Esto no solo es un fenómeno interesante desde el punto de vista matemático, sino que también tiene aplicaciones prácticas en diversos campos como la física, la ingeniería y las ciencias de la computación.

Relación con el movimiento armónico simple

Otra curiosidad relacionada con la función seno es su estrecha relación con el concepto de movimiento armónico simple (MAS). El MAS es un tipo de movimiento vibratorio que se caracteriza por tener una trayectoria sinusoidal, similar a la forma de la función seno.

En el MAS, un objeto se desplaza hacia adelante y hacia atrás en torno a una posición de equilibrio, siguiendo una trayectoria sinusoidal. La amplitud de esta trayectoria está relacionada con el valor máximo que alcanza el seno, mientras que la frecuencia está asociada con la velocidad a la que se repite el movimiento.

Esta relación entre el MAS y la función seno es especialmente relevante en disciplinas como la física y la ingeniería, donde se utilizan modelos basados en el MAS para describir el comportamiento de sistemas oscilantes como resortes, péndulos y circuitos eléctricos.

La función seno en la música y el arte

Además de su importancia en el ámbito científico y matemático, la función seno también ha influido en otras áreas creativas como la música y el arte visual.

En la música, la función seno se relaciona con las ondas sonoras y permite generar diferentes tonalidades y timbres. Por ejemplo, la forma en que se combinan las distintas frecuencias sinusoidales en una melodía determina su sonoridad y calidad auditiva. Esta relación entre la función seno y la música ha permitido desarrollar técnicas de síntesis de sonido y diseño de instrumentos musicales.

Por otro lado, el arte visual también ha encontrado inspiración en la función seno y sus características estéticas. La forma sinuosa y armónica de la función seno ha sido utilizada por artistas para crear líneas curvas, patrones y composiciones visuales interesantes. Incluso, algunos artistas han experimentado con representaciones gráficas de la función seno en sus obras, explorando su belleza matemática y su potencial expresivo.

Otras aplicaciones de la función seno

Además de las curiosidades mencionadas anteriormente, la función seno tiene numerosas aplicaciones prácticas en diversos campos.

En la física, por ejemplo, el seno se utiliza para describir fenómenos ondulatorios como la propagación de ondas luminosas y sonoras, así como también en el estudio de la interferencia y la difracción. En la ingeniería eléctrica, el seno es fundamental para comprender el comportamiento de los circuitos de corriente alterna, ya que permite analizar sus características, como la amplitud y la frecuencia.

Asimismo, en las ciencias de la computación, el seno también encuentra aplicaciones en campos como la criptografía y el procesamiento digital de señales, donde su periodicidad y propiedades matemáticas son aprovechadas para desarrollar algoritmos y codificaciones seguras.

La función seno es un concepto fascinante que va más allá de ser una simple operación matemática. Su comportamiento periódico, su relación con el movimiento armónico simple, su influencia en la música y el arte, así como sus amplias aplicaciones en distintas disciplinas, hacen de la función seno una de las herramientas más versátiles y poderosas de las matemáticas.

Cómo se puede calcular el valor de la función seno para un ángulo específico

La función seno es una de las funciones trigonométricas más utilizadas en matemáticas y ciencias. Permite relacionar un ángulo con el valor del seno de ese ángulo. Calcular el valor del seno para un ángulo específico puede parecer complicado al principio, pero existen varias formas de hacerlo.

1. Calculadora científica

Una forma sencilla de calcular el valor del seno de un ángulo es utilizando una calculadora científica. La mayoría de las calculadoras modernas cuentan con una función seno (sin) que permite ingresar el valor del ángulo en radianes o grados y obtener el resultado rápidamente. Solo tienes que asegurarte de que tu calculadora esté configurada en el modo correcto (radianes o grados) y ingresar el ángulo deseado.

2. Fórmula matemática

Otra forma de calcular el valor del seno es utilizando la fórmula matemática correspondiente. En trigonometría, se define el seno de un ángulo como la razón entre la longitud del cateto opuesto y la hipotenusa en un triángulo rectángulo. Esta fórmula se expresa de la siguiente manera:

sen(θ) = (cateto_opuesto / hipotenusa)

Para utilizar esta fórmula, primero necesitas identificar el ángulo en cuestión y construir un triángulo rectángulo que contenga dicho ángulo. Luego, mide la longitud del cateto opuesto y la hipotenusa y sustituye estos valores en la fórmula.

3. Tablas de valores

Otra opción es utilizar tablas de valores precalculados del seno para diferentes ángulos. Estas tablas suelen estar disponibles en libros de referencia matemática o en línea. Puedes buscar el ángulo específico en la tabla y encontrar el valor correspondiente del seno. Aunque esta opción puede ser menos precisa que las anteriores, es útil cuando necesitas una aproximación rápida sin tener que hacer cálculos extensos.

Recuerda que el valor del seno puede oscilar entre -1 y 1, dependiendo del ángulo. Los ángulos de 0°, 90°, 180°, 270° y 360° tienen valores especiales, por lo que puedes memorizarlos para facilitar los cálculos:

• sen(0°) = 0
• sen(90°) = 1
• sen(180°) = 0
• sen(270°) = -1
• sen(360°) = 0

Con estas diferentes opciones, podrás calcular fácilmente el valor del seno para cualquier ángulo específico. Recuerda practicar con ejercicios y problemas para mejorar tu comprensión y habilidades en el cálculo del seno.

Cuál es la importancia de comprender el rango de la función seno en campos como la física y la ingeniería

La comprensión del rango de la función seno es de vital importancia en campos como la física y la ingeniería, ya que esta función desempeña un papel fundamental en el análisis y modelado de fenómenos periódicos. El rango de la función seno abarca un espectro completo de valores, desde -1 hasta 1, lo que significa que puede representar una amplia variedad de comportamientos oscilatorios.

En física, el estudio de las ondas y vibraciones se basa en gran medida en el análisis de funciones trigonométricas como el seno. En particular, el rango de la función seno permite describir con precisión la amplitud y frecuencia de una onda, lo cual es crucial en campos como acústica, óptica y electromagnetismo. Por ejemplo, al analizar el comportamiento de una onda sonora, podemos utilizar la función seno para determinar su volumen, tono y duración.

En ingeniería, el conocimiento del rango de la función seno es esencial para el diseño y control de sistemas que involucran movimientos oscilatorios. Por ejemplo, en robótica, el uso de funciones senoidales permite programar movimientos suaves y precisos de los brazos o extremidades de un robot. Asimismo, en telecomunicaciones, el rango de la función seno es utilizado para modular señales y transmitir información a través de diferentes tipos de ondas.

Otro campo en el que la comprensión del rango de la función seno resulta fundamental es en la resolución de problemas de matemáticas aplicadas. Muchos fenómenos físicos y naturales pueden ser representados mediante funciones senoidales, y al comprender el rango de la función seno, podemos modelar con precisión estos fenómenos y resolver ecuaciones diferenciales que describen su comportamiento.

Comprender el rango de la función seno es esencial en campos como la física y la ingeniería debido a su capacidad para describir fenómenos oscilatorios. La amplitud y frecuencia de una onda, el diseño de sistemas de control y la resolución de problemas matemáticos son solo algunas de las aplicaciones donde el conocimiento del rango de la función seno resulta crucial. Así que, ¡sumérgete en este fascinante mundo de infinitas posibilidades y descubre cómo el seno puede ayudarte a entender el universo que nos rodea!

El valor del seno de un ángulo se calcula dividiendo la longitud del cateto opuesto al ángulo entre la hipotenusa en un triángulo rectángulo.

El resultado del seno no tiene unidades específicas, ya que es una razón entre longitudes y se expresa como un número puro.

El rango de valores posibles para el seno está entre -1 y 1, inclusivo. El valor mínimo (-1) se alcanza cuando el ángulo es de 270 grados o π radianes, y el valor máximo (1) se alcanza cuando el ángulo es de 90 grados o π/2 radianes.

El seno se utiliza en campos como la física, la ingeniería y la arquitectura para calcular fuerzas, tensiones, movimientos oscilatorios y dimensiones de estructuras triangulares.

El seno y el coseno son funciones trigonométricas relacionadas entre sí. El seno de un ángulo se define como la razón entre el cateto opuesto y la hipotenusa de un triángulo rectángulo, mientras que el coseno se define como la razón entre el cateto adyacente y la hipotenusa.