¡Descubre cómo son las áreas de estos triángulos y aumenta tus conocimientos matemáticos!

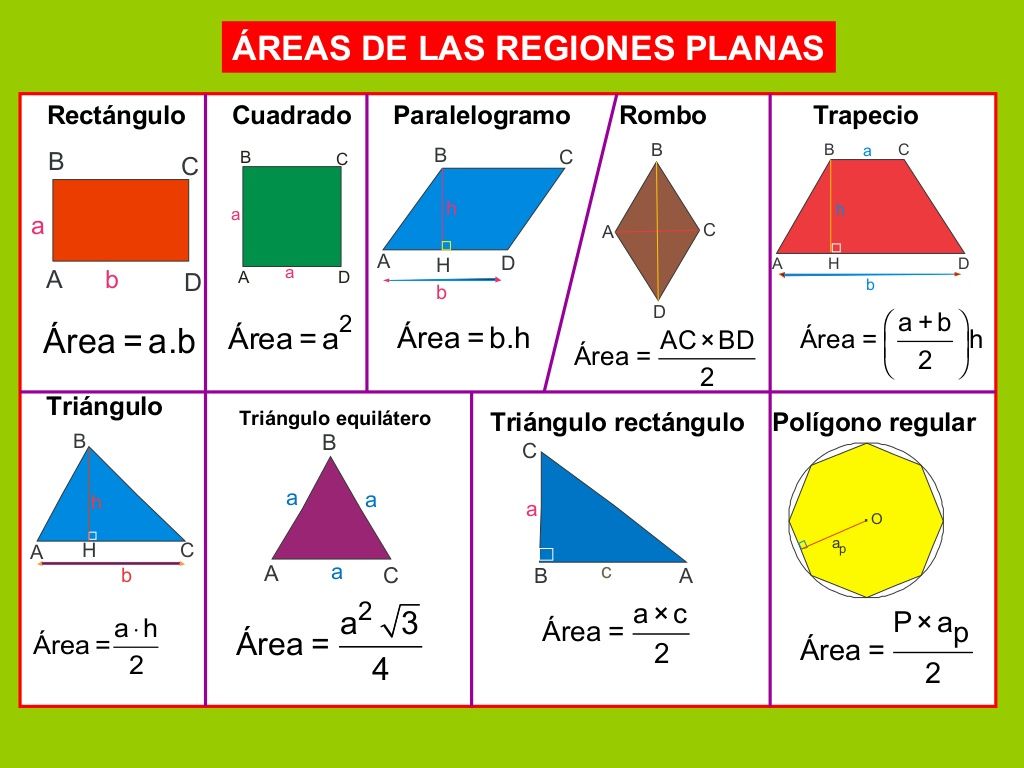
Los triángulos son figuras geométricas muy conocidas y estudiadas en las matemáticas. Se caracterizan por tener tres lados y tres ángulos, y pueden clasificarse en diferentes tipos según sus características. Entre esas características, una de las más importantes es su área, que nos permite calcular la cantidad de espacio ocupado por el triángulo dentro de un plano.

En este artículo exploraremos las fórmulas para calcular el área de diferentes tipos de triángulos, como el triángulo equilátero, el triángulo isósceles, el triángulo rectángulo y el triángulo escaleno. Además, veremos ejemplos prácticos para entender mejor cómo aplicar estas fórmulas en problemas reales. Así que prepárate para aprender y descubrir los secretos de las áreas de los triángulos.

Qué es un área y cómo se calcula en matemáticas

El concepto de área es fundamental en matemáticas y se utiliza para medir la extensión de una figura plana. En términos sencillos, el área de una figura representa la cantidad de espacio que ocupa dentro de ella. Es una medida bidimensional que nos permite comparar y analizar diferentes formas geométricas.

Para calcular el área de una figura, es necesario utilizar fórmulas específicas dependiendo del tipo de figura que estemos tratando. En el caso de los triángulos, existen diferentes métodos para determinar su área según las características que conozcamos de ellos.

Uno de los métodos más comunes para calcular el área de un triángulo es a través de la fórmula clásica: A = (base * altura) / 2. En esta fórmula, la base se refiere a uno de los lados del triángulo sobre el cual se mide la distancia perpendicular hasta el vértice opuesto, conocida como altura.

Sin embargo, es importante destacar que no siempre contamos con la base y la altura conocidas. En algunos casos, podemos tener información limitada, como por ejemplo los valores de los tres lados del triángulo o los ángulos internos. Para estos escenarios, existen otras fórmulas y teoremas que nos permiten calcular el área de manera precisa.

Otro método para calcular el área de un triángulo es mediante la fórmula conocida como "Fórmula general de Herón". Esta fórmula utiliza únicamente las longitudes de los tres lados del triángulo, lo cual puede resultar útil cuando no disponemos de la base y altura como datos.

Además de estas fórmulas clásicas, en matemáticas existen otros teoremas y métodos avanzados para determinar el área de triángulos con características especiales, como los triángulos equiláteros, isósceles o rectángulos. Estos teoremas, basados en propiedades geométricas y trigonométricas, nos permiten calcular el área con mayor precisión y eficiencia.

El cálculo del área no solo es útil en matemáticas, sino que tiene aplicaciones prácticas en nuestro día a día. Por ejemplo, al construir una casa, necesitamos saber el área de los cuartos y espacios para dimensionar correctamente los materiales. En la agricultura, se utiliza para determinar el área de terrenos y saber cuántas plantas pueden ser sembradas en un espacio determinado.

Entender qué es un área y cómo se calcula en matemáticas es fundamental para comprender el mundo que nos rodea y realizar cálculos precisos en diversas áreas de estudio. Ya sea utilizando fórmulas clásicas, teoremas especializados o métodos avanzados, el cálculo del área de un triángulo nos brinda información valiosa para resolver problemas y aumentar nuestros conocimientos matemáticos.

Cómo calcular el área de un triángulo

Calcular el área de un triángulo es una habilidad básica en matemáticas que todos deberíamos dominar. El área de un triángulo se puede calcular utilizando diferentes fórmulas, dependiendo de la información que tengamos sobre el triángulo. En este artículo, te mostraré algunas de las formas más comunes de calcular el área de un triángulo y te daré ejemplos prácticos para que puedas entender mejor los conceptos.

Fórmula del área de un triángulo equilátero

Un triángulo equilátero es aquel que tiene todos sus lados iguales. Para calcular el área de un triángulo equilátero, podemos utilizar la siguiente fórmula:

Área = (lado)^2 * (√3 / 4)

Donde "lado" es la longitud de cualquiera de los lados del triángulo. Por ejemplo, si tenemos un triángulo equilátero con un lado de longitud 6 cm, podemos calcular su área de la siguiente manera:

Área = (6)^2 * (√3 / 4) = 36 * (√3 / 4) ≈ 15.588 cm^2

Fórmula del área de un triángulo rectángulo

Un triángulo rectángulo es aquel que tiene uno de sus ángulos rectos, es decir, de 90 grados. Para calcular el área de un triángulo rectángulo, podemos utilizar la siguiente fórmula:

Área = (base * altura) / 2

Donde "base" es la longitud de la base del triángulo y "altura" es la longitud de la altura que forma un ángulo recto con la base. Supongamos que tenemos un triángulo rectángulo con una base de 8 cm y una altura de 5 cm, podemos calcular su área de la siguiente manera:

Área = (8 * 5) / 2 = 40 / 2 = 20 cm^2

Fórmula del área de un triángulo cualquiera

Para calcular el área de un triángulo cualquiera, es decir, aquel que no es equilátero ni rectángulo, podemos utilizar la fórmula de Herón. La fórmula de Herón se basa en los lados del triángulo y se define de la siguiente manera:

Área = √(s * (s - a) * (s - b) * (s - c))

Donde "a", "b" y "c" son las longitudes de los lados del triángulo, y "s" se conoce como semiperímetro y se calcula sumando los tres lados y dividiendo entre 2:

s = (a + b + c) / 2

Supongamos que tenemos un triángulo con lados de longitud 7 cm, 9 cm y 12 cm. Podemos calcular su área utilizando la fórmula de Herón de la siguiente manera:

s = (7 + 9 + 12) / 2 = 28 / 2 = 14
Área = √(14 * (14 - 7) * (14 - 9) * (14 - 12)) = √(14 * 7 * 5 * 2) ≈ √980 ≈ 31.304 cm^2

Como puedes ver, calcular el área de un triángulo no es tan complicado si conoces las fórmulas adecuadas. Recuerda que siempre debes tener en cuenta la información que tienes sobre el triángulo antes de aplicar una fórmula específica. ¡Practica con diferentes tipos de triángulos y aumenta tus conocimientos matemáticos!

Cuáles son las fórmulas para calcular el área de diferentes tipos de triángulos

El área de un triángulo es una medida importante en matemáticas y geometría. Determinar correctamente el área de un triángulo puede ser crucial para resolver problemas y aplicaciones que involucren estas figuras geométricas.

Existen diferentes fórmulas para calcular el área de los distintos tipos de triángulos, cada una adaptada a las características particulares de cada tipo. A continuación, te presentaré algunas de las fórmulas más comunes:

Área del triángulo equilátero

Un triángulo equilátero es aquél cuyos tres lados tienen la misma longitud. Para calcular su área, se utiliza la siguiente fórmula:

Área = (lado^2 * √3) / 4

Área del triángulo isósceles

Un triángulo isósceles es aquel que tiene dos lados iguales y uno diferente. Para calcular su área, se utiliza la siguiente fórmula:

Área = (base * altura) / 2

Área del triángulo escaleno

Un triángulo escaleno es aquel que tiene sus tres lados con longitudes diferentes. Para calcular su área, se utiliza la fórmula conocida como la fórmula de Herón:

Área = √(s * (s - lado1) * (s - lado2) * (s - lado3))

Donde "s" representa el semiperímetro del triángulo, es decir:

s = (lado1 + lado2 + lado3) / 2

Área del triángulo rectángulo

Un triángulo rectángulo es aquel que tiene un ángulo recto en su interior. Para calcular su área, se utiliza la siguiente fórmula:

Área = (base * altura) / 2

donde la base y la altura corresponden a los lados que forman el ángulo recto.

Ahora que conoces las fórmulas para calcular el área de distintos tipos de triángulos, podrás aplicar estos conocimientos en problemas geométricos y mejorar tus habilidades matemáticas.

Cómo encontrar la altura de un triángulo si conocemos su área y la longitud de una base

En matemáticas, el estudio de los triángulos es fundamental para comprender numerosos conceptos y teoremas. Uno de los elementos clave en la geometría triangular es la altura de un triángulo, ya que nos permite determinar la superficie encerrada por sus lados.

Existen diferentes métodos para encontrar la altura de un triángulo, dependiendo de la información que se conozca. En este caso, nos enfocaremos en cómo calcular la altura si conocemos el área del triángulo y la longitud de una de sus bases.

Para hacer esto, podemos utilizar la siguiente fórmula:

Altura = (2 * Área) / Base

Donde "Área" corresponde al área del triángulo y "Base" representa la longitud de la base conocida. La fórmula se basa en relaciones proporcionales entre los elementos del triángulo.

Supongamos que tenemos un triángulo con un área de 36 unidades cuadradas y una base de longitud 9 unidades. Podemos aplicar la fórmula de la altura de la siguiente manera:

Altura = (2 * 36) / 9 = 8 unidades

Por lo tanto, la altura de este triángulo sería de 8 unidades.

Es importante destacar que, para utilizar esta fórmula, es necesario conocer la medida exacta del área del triángulo y la longitud de una base. Si solo se tienen estimaciones o aproximaciones, los resultados obtenidos pueden ser inexactos.

Calcular la altura de un triángulo a partir del área y la longitud de una base puede ser útil en diversos contextos, como la arquitectura, la ingeniería o la resolución de problemas geométricos. Es una herramienta que nos permite determinar dimensiones desconocidas a partir de información limitada.

Conocer cómo encontrar la altura de un triángulo utilizando el área y la longitud de una base nos brinda una poderosa herramienta para analizar y comprender la geometría de estas figuras. La fórmula mencionada anteriormente nos ayudará a resolver problemas asociados con triángulos y ampliar nuestros conocimientos matemáticos.

Cuáles son las propiedades de los triángulos equiláteros en relación a sus áreas

Los triángulos equiláteros son un tipo especial de triángulo que tiene todas sus partes iguales en longitud. Esto significa que todos sus lados y ángulos internos son exactamente iguales entre sí. Su simetría y uniformidad los convierten en una figura geométrica muy interesante para estudiar.

Cuando se trata de las áreas de los triángulos equiláteros, hay ciertas propiedades importantes que debemos tener en cuenta. La fórmula básica para calcular el área de cualquier triángulo es 1/2 x base x altura. Sin embargo, en el caso de los triángulos equiláteros, podemos utilizar una fórmula más específica y simplificada.

Fórmula del área de un triángulo equilátero

La fórmula para calcular el área de un triángulo equilátero es bastante sencilla. Solo necesitamos conocer la longitud de uno de sus lados para poder determinar su área. La fórmula es la siguiente:

Área = (lado^2 * √3) / 4

Donde "lado" representa la longitud de uno de los lados del triángulo equilátero.

Esta fórmula se deriva de una serie de propiedades y relaciones matemáticas relacionadas con los triángulos equiláteros. Una de ellas es que los ángulos internos de un triángulo equilátero siempre miden 60 grados, lo que nos permite utilizar trigonometría para sacar la fórmula del área.

La razón por la que esta fórmula es tan sencilla y práctica es porque se basa en el hecho de que, para un triángulo equilátero dado, su altura es igual a la raíz cuadrada de 3/2 veces su longitud. Esto puede parecer complicado, pero gracias a esta relación podemos determinar fácilmente el área utilizando solo la longitud de uno de sus lados.

Ejemplo de cálculo del área

Para entender mejor cómo utilizar esta fórmula, veamos un ejemplo. Supongamos que tenemos un triángulo equilátero con un lado de longitud 6 cm. Podemos calcular su área de la siguiente manera:

Área = (6^2 * √3) / 4
Área = (36 * √3) / 4
Área = 9√3 cm^2

Por lo tanto, el área de este triángulo equilátero específico sería de 9√3 centímetros cuadrados.

Este ejemplo nos muestra cómo podemos aplicar la fórmula del área de un triángulo equilátero en la práctica. Es importante destacar que esta fórmula no solo se aplica a los triángulos equiláteros perfectos, sino también a aquellos que son aproximadamente equiláteros o tienen lados muy cercanos en longitud.

Las propiedades de los triángulos equiláteros en relación a sus áreas son muy específicas y se pueden calcular fácilmente utilizando una fórmula determinada. Con el conocimiento de la longitud de uno de los lados, podemos obtener el área de manera rápida y precisa. Estudiar las áreas de los triángulos equiláteros es una forma interesante de incrementar nuestros conocimientos matemáticos y comprender mejor las propiedades de esta figura geométrica tan especial.

Cuál es el área de un triángulo rectángulo con catetos de longitudes dadas

En matemáticas, el área de un triángulo rectángulo se puede calcular fácilmente si conocemos las longitudes de sus catetos. En este artículo, te mostraremos cómo puedes determinar el área de un triángulo rectángulo cuando tienes los valores de ambos catetos.

Antes de sumergirnos en los cálculos, recordemos que un triángulo rectángulo es aquel que tiene un ángulo recto, es decir, un ángulo de 90 grados. Los dos lados que forman el ángulo recto se llaman catetos, mientras que el lado opuesto al ángulo recto se conoce como hipotenusa.

Para calcular el área de un triángulo rectángulo, utilizamos la fórmula:

Área = (base * altura) / 2

En este caso, la base y la altura del triángulo son los catetos. Entonces, si conocemos la longitud de ambos catetos, podemos sustituir estos valores en la fórmula y calcular el área.

Ejemplo práctico: área de un triángulo rectángulo con catetos de 5 cm y 3 cm

Supongamos que tenemos un triángulo rectángulo con un cateto de 5 centímetros de longitud y otro cateto de 3 centímetros de longitud. Vamos a calcular su área utilizando la fórmula mencionada anteriormente.

Sustituyendo los valores en la fórmula, obtenemos:

Área = (5 * 3) / 2

Simplificando la multiplicación y dividendo, tenemos:

Área = 15 / 2

Finalmente, calculando el resultado, obtenemos:

Área = 7.5 cm²

Por lo tanto, el área de este triángulo rectángulo con catetos de 5 cm y 3 cm es de 7.5 centímetros cuadrados.

Es importante resaltar que siempre debemos recordar las unidades de medida al calcular el área, ya que el resultado debe expresarse en unidades cuadradas. Además, recuerda que esta fórmula solo es válida para triángulos rectángulos, por lo que no se puede utilizar en otros tipos de triángulos.

Ahora que sabes cómo calcular el área de un triángulo rectángulo con catetos dados, ¡puedes poner en práctica tus conocimientos matemáticos! Recuerda practicar con diferentes valores de catetos y mejora tus habilidades en geometría.

Cómo calcular el área de un triángulo isósceles o escaleno

Calcular el área de un triángulo es una tarea fundamental en matemáticas. Si bien existen diferentes fórmulas para calcular el área según el tipo de triángulo, en este artículo nos enfocaremos en los triángulos isósceles y escalenos.

Triángulo isósceles

Un triángulo isósceles es aquel que tiene dos lados iguales y un lado diferente. Para calcular el área de este tipo de triángulo, se puede utilizar la fórmula del área de un triángulo general, que es base por altura dividido por 2.

A = (base * altura) / 2

En el caso del triángulo isósceles, la base será uno de los dos lados iguales y la altura corresponderá a la distancia desde la base hasta el vértice opuesto.

Una forma común de encontrar la altura de un triángulo isósceles es utilizando el teorema de Pitágoras. Si conoces las longitudes de los dos lados iguales y quieres encontrar la altura, puedes aplicar la siguiente fórmula:

altura = √(lado^2 - (base/2)^2)

Una vez que hayas calculado la altura, simplemente sustitúyela en la fórmula del área y obtendrás el resultado deseado.

Triángulo escaleno

El triángulo escaleno es aquel en el que todos sus lados tienen longitudes diferentes. En este caso, el cálculo del área requiere de otra fórmula, conocida como la fórmula de Herón.

A = √(s(s-a)(s-b)(s-c))

Donde a, b y c son las longitudes de los lados del triángulo, y s es el semiperímetro, que se calcula sumando las longitudes de los tres lados y dividiendo por 2:

s = (a + b + c) / 2

Una vez que hayas calculado el valor de s, puedes sustituirlo en la fórmula de Herón para obtener el área del triángulo escaleno.

Recuerda que estas fórmulas son útiles para calcular el área de los triángulos isósceles y escalenos. Si te encuentras con otros tipos de triángulos, como el equilátero o el rectángulo, existen fórmulas específicas para calcular sus áreas. ¡No dudes en investigar más sobre el fascinante mundo de las matemáticas!

Cuál es el área de un triángulo si conocemos las longitudes de sus lados pero no podemos trazar una altura

Calcular el área de un triángulo puede parecer una tarea sencilla cuando tenemos todas las medidas necesarias, pero ¿qué sucede cuando solo conocemos las longitudes de sus lados y no podemos trazar una altura? En esta sección, exploraremos cómo encontrar el área de un triángulo sin tener los datos convencionales.

Para resolver este problema, podemos recurrir a la fórmula conocida como "fórmula de Herón". Esta fórmula se basa en el semiperímetro del triángulo (la mitad de la suma de las longitudes de los lados) y las longitudes de los lados del triángulo. Su expresión matemática es la siguiente:

Área = √(s*(s-a)*(s-b)*(s-c))

En esta fórmula, a, b y c representan las longitudes de los lados del triángulo, mientras que s es el semiperímetro. Para obtener el área del triángulo, necesitamos calcular el valor de s primero. Podemos hacerlo sumando los tres lados y dividiendo esa suma entre 2:

s = (a + b + c) / 2

Una vez que tengamos el valor de s, podemos aplicarlo en la fórmula de Herón para encontrar el área del triángulo con las longitudes de los lados dados.

Veamos un ejemplo práctico para comprender mejor el proceso. Supongamos que tenemos un triángulo con longitudes de lados de 5, 7 y 9 unidades respectivamente. Primero, calculamos el semiperímetro:

s = (5 + 7 + 9) / 2 = 21 / 2 = 10.5

Ahora, podemos usar este valor en la fórmula de Herón para encontrar el área:

Área = √(10.5 * (10.5 - 5) * (10.5 - 7) * (10.5 - 9)) ≈ √(10.5 * 5.5 * 3.5 * 1.5) ≈ √726.5625 ≈ 26.97

Por lo tanto, el área de este triángulo en particular sería aproximadamente 26.97 unidades cuadradas.

Es importante destacar que la fórmula de Herón solo funciona para triángulos con medidas de lados que cumplan con la desigualdad triangular, es decir, la suma de las longitudes de dos de sus lados debe ser siempre mayor que la longitud del tercer lado. Si estos valores no se cumplen, la fórmula de Herón no será válida y deberemos buscar otro método para calcular el área.

Ahora que conoces la fórmula de Herón y cómo aplicarla, podrás calcular fácilmente el área de triángulos incluso cuando no tengas información sobre sus alturas. Amplía tus conocimientos matemáticos y experimenta con diferentes triángulos usando esta fórmula. ¡Diviértete descubriendo el mundo de las figuras geométricas!

Cuál es el área del triángulo más grande que puede encajar en un círculo dado

El cálculo del área de un triángulo es fundamental en matemáticas y tiene aplicaciones tanto en geometría como en trigonometría. Pero, ¿alguna vez te has preguntado cuál es el máximo tamaño que puede tener un triángulo dentro de un círculo dado?

Para responder a esta pregunta, primero tenemos que entender algunas propiedades de los triángulos y los círculos. Un triángulo inscrito en un círculo se llama triángulo circunscrito, y tiene la particularidad de que sus tres vértices están en la circunferencia del círculo.

La clave para determinar el área máxima de un triángulo inscrito en un círculo es el teorema de Pitágoras. Según este teorema, en un triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa. Ahora, si consideramos uno de los catetos como el diámetro de la circunferencia circunscrita al triángulo, podemos relacionar sus lados usando el radio del círculo (la mitad del diámetro).

Supongamos que el radio del círculo es r. Entonces, el lado opuesto al ángulo recto en el triángulo rectángulo será r, el cateto adyacente será r/2 y la hipotenusa será r√5/2, por el teorema de Pitágoras. Así, hemos encontrado las longitudes de los lados del triángulo inscrito en un círculo de radio r.

Para calcular el área de este triángulo, podemos usar la fórmula del área de un triángulo dada por (base * altura) / 2. En nuestro caso, la base es r/2 y la altura es r√5/2. Sustituyendo estos valores en la fórmula, obtenemos un área máxima de (r^2√5)/8.

Esta fórmula nos permite calcular rápidamente el área del triángulo más grande que puede encajar en un círculo dado en función de su radio. Además, si consideramos diferentes radios, podemos observar una relación interesante: a medida que aumenta el radio del círculo, el área del triángulo también aumenta, pero no de manera proporcional. De hecho, el área aumenta más rápidamente que el radio, lo que significa que a medida que el círculo se hace más grande, el triángulo inscrito crece aún más en área.

El área del triángulo más grande que puede encajar en un círculo dado está determinada por la fórmula (r^2√5)/8, donde r es el radio del círculo. Este concepto es fundamental en geometría y tiene aplicaciones en campos como la arquitectura y los sistemas de posicionamiento global (GPS).

... (continúa con el resto del artículo) ...

Cómo aplicar el concepto de área de triángulos en problemas del mundo real

Los triángulos son una de las figuras geométricas más fundamentales y versátiles en matemáticas. Su estudio es crucial para comprender diferentes aspectos de la geometría y también tiene aplicaciones prácticas en el mundo real. Una de las principales características de los triángulos que se estudia en matemáticas es su área.

¿Qué es el área de un triángulo?

El área de un triángulo es la medida de la región bidimensional encerrada por sus tres lados. Es una medida importante ya que puede proporcionar información valiosa sobre el tamaño y la forma de un triángulo en relación con otros objetos o áreas.

En términos más técnicos, el área de un triángulo se calcula multiplicando la longitud de una base del triángulo por su altura y dividiendo el resultado por dos, utilizando la fórmula clásica del área: Área = (base * altura) / 2.

Es importante destacar que tanto la base como la altura del triángulo deben estar perpendiculares entre sí, es decir, deben formar un ángulo de 90 grados. En caso contrario, será necesario utilizar otras fórmulas o métodos para calcular el área.

Aplicaciones del concepto de área de triángulos

Aunque puede parecer que el cálculo del área de un triángulo solo tiene relevancia dentro del ámbito matemático, esta medida se encuentra presente en diversas situaciones y problemas del mundo real.

Por ejemplo, en la arquitectura y la ingeniería civil, el cálculo del área de un triángulo es esencial para determinar la cantidad de materiales necesarios para construir estructuras con forma triangular, como techos o puentes. También se utiliza en la planificación urbana y la topografía para calcular áreas de terrenos y parcelas, lo que facilita la distribución eficiente de infraestructuras y edificaciones.

En los campos de la física y la geometría analítica, el área de un triángulo se aplica en problemas de cálculo integral y en la determinación de vectores y direcciones en espacios tridimensionales.

Ejemplos prácticos de cálculo de áreas de triángulos

Para comprender mejor cómo se utiliza el concepto de área de triángulos en situaciones cotidianas, consideremos algunos ejemplos:

• Un diseñador de modas necesita calcular el área de un triángulo para diseñar correctamente la forma de un vestido o una falda.
• Un carpintero necesita determinar el área de un triángulo para cortar piezas de madera y construir muebles o marcos.
• Un agrimensor utiliza el cálculo del área de un triángulo para medir terrenos y parcelas en trabajos de levantamiento topográfico.
• Un arquitecto necesita calcular el área de un triángulo para diseñar con precisión la forma de un techo en un edificio.

Como se puede ver, el concepto de área de triángulos es fundamental en una amplia variedad de campos y actividades. Conocer cómo calcular esta medida no solo amplía nuestros conocimientos matemáticos, sino que también nos ayuda a entender mejor el mundo que nos rodea y nos ofrece herramientas para resolver problemas de manera más efectiva.

Preguntas frecuentes (FAQ)

1. ¿Cómo puedo calcular el área de un triángulo?

Para calcular el área de un triángulo, puedes usar la fórmula A = (base x altura) / 2.

2. ¿Qué es la base de un triángulo?

La base de un triángulo es el lado horizontal sobre el cual se levanta el triángulo. Es uno de los lados del triángulo.

3. ¿Cómo puedo encontrar la altura de un triángulo si no la sé?

Puedes utilizar la fórmula de área de un triángulo para despejar la altura: altura = (2 x área) / base. Debes conocer la base y el área para poder encontrar la altura.

4. ¿Qué tipos de triángulos tienen áreas especiales?

Los triángulos equiláteros y los triángulos rectángulos tienen áreas especiales. En un triángulo equilátero, el área es A = (lado^2 x √3) / 4, y en un triángulo rectángulo, es A = (base x altura) / 2.

5. ¿Se puede calcular el área de un triángulo si solo conozco sus lados?

No es posible calcular el área de un triángulo solo conociendo sus lados. Además de los lados, necesitas conocer la altura o la base del triángulo para poder calcular su área correctamente.