¡Desbloquea el misterio del ángulo central de un polígono con estos cinco pasos infalibles!

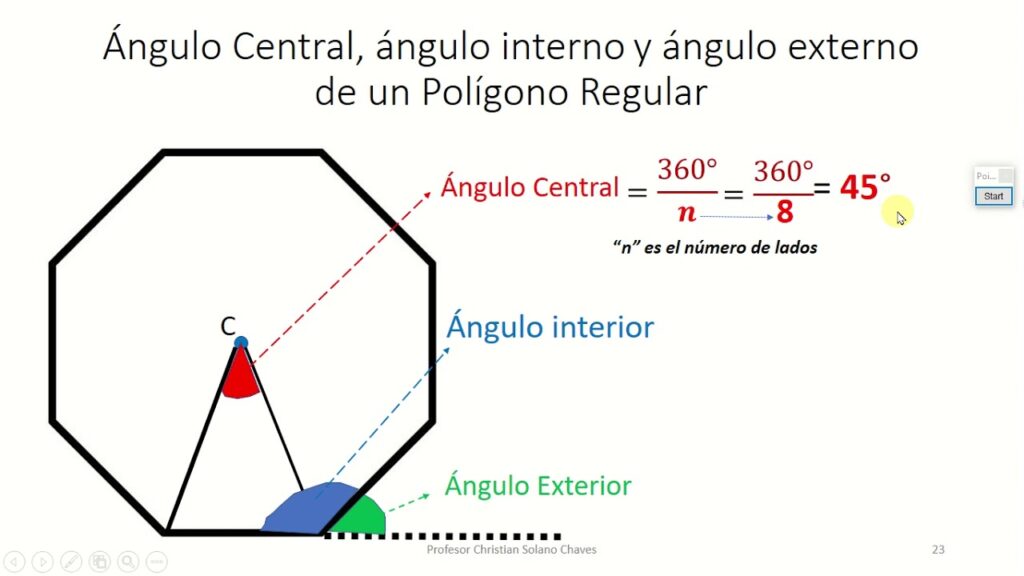
El ángulo central de un polígono es un concepto fundamental en geometría que nos permite comprender mejor las propiedades y características de las figuras geométricas. Un ángulo central es aquel formado por dos radios que parten del centro de un polígono hacia sus vértices. El tamaño de este ángulo central depende del número de lados del polígono, lo que lo convierte en una herramienta esencial para el cálculo y la medición de los ángulos internos de una figura.

Te presentaremos cinco pasos infalibles para desbloquear el misterio del ángulo central de cualquier polígono. Te explicaremos cómo calcular su valor exacto y cómo utilizarlo para determinar otros ángulos internos. Además, te mostraremos ejemplos prácticos para que puedas aplicar estos conceptos a diferentes tipos de polígonos. ¡Prepárate para descubrir un nuevo mundo de geometría con el estudio del ángulo central!

Qué es el ángulo central de un polígono

El ángulo central de un polígono es uno de los conceptos más importantes en la geometría. Es el ángulo formado por dos radios trazados desde el centro del polígono hacia dos vértices adyacentes. En otras palabras, es el ángulo que se forma en el centro del polígono cuando se trazan segmentos desde el centro hasta cada uno de los vértices.

Este ángulo es fundamental porque nos proporciona información valiosa sobre la medida de los ángulos internos de un polígono. Saber cómo calcular el ángulo central nos permite desbloquear el misterio de los demás ángulos y propiedades del polígono.

Cómo calcular el ángulo central paso a paso

Ahora que entendemos qué es el ángulo central, veamos cómo podemos calcularlo paso a paso. Sigue estos cinco pasos infalibles para desbloquear el misterio del ángulo central de cualquier polígono:

1. Identifica el polígono: Lo primero que debes hacer es identificar el tipo de polígono del que quieres calcular el ángulo central. Ya sea un triángulo, cuadrilátero, pentágono o cualquier otro, asegúrate de conocer el número de lados del polígono.
2. Encuentra el ángulo exterior: Para calcular el ángulo central, necesitamos conocer el ángulo exterior del polígono. El ángulo exterior es aquel que se forma entre una línea que conecta dos vértices y la prolongación de otra línea que parte de uno de esos vértices. Utiliza la fórmula 360° / n para calcular el ángulo exterior, donde "n" es el número de lados del polígono.
3. Calcula el ángulo central: El ángulo central será igual al ángulo exterior dividido por dos. Esto se debe a que el ángulo central y el ángulo exterior son suplementarios, es decir, suman 180 grados. Por lo tanto, si conocemos el ángulo exterior, podemos determinar fácilmente el ángulo central.
4. Verifica la medida del ángulo central: Una vez que hayas calculado el ángulo central, asegúrate de verificar su medida. Recuerda que la suma de los ángulos centrales de un polígono siempre es igual a 360 grados. Puedes sumar todos los ángulos centrales de los lados del polígono para confirmar que obtienes el resultado esperado.
5. Aplica el ángulo central en problemas de geometría: Ahora que sabes cómo calcular el ángulo central de un polígono, puedes aplicarlo en diferentes problemas de geometría. Utilízalo para encontrar medidas desconocidas, determinar congruencia entre polígonos o resolver ecuaciones relacionadas con ángulos internos y externos.

¡Con estos cinco pasos infalibles, podrás desbloquear el misterio del ángulo central de cualquier polígono! Aprovecha este conocimiento para profundizar tu comprensión de la geometría y explorar las infinitas posibilidades que ofrece esta fascinante disciplina.

Por qué es importante conocer el ángulo central de un polígono

El ángulo central de un polígono es uno de los conceptos más fundamentales en geometría. Es la medida del ángulo formado por dos radios trazados desde el centro del polígono hacia dos vértices consecutivos. Comprender y poder calcular este ángulo es crucial para resolver una variedad de problemas geométricos, desde encontrar áreas hasta determinar propiedades y características específicas de los polígonos.

Conocer el ángulo central nos permite desbloquear un mundo de posibilidades geométricas. Podemos utilizar esta información para calcular otros ángulos dentro del polígono, determinar cuántos lados tiene un polígono desconocido o incluso identificar si un polígono es regular o irregular. El ángulo central es como una clave maestra que nos brinda acceso a un tesoro oculto de conocimiento geométrico.

Cinco pasos infalibles para calcular el ángulo central de un polígono

1. Paso 1: Identifica el número de lados del polígono. Puede ser un triángulo, un cuadrilátero, un pentágono, un hexágono o cualquier otro polígono con múltiples lados.
2. Paso 2: Divide 360 grados entre el número de lados del polígono. Esto te dará la medida del ángulo central de cada lado.
3. Paso 3: Si el polígono es regular, lo cual significa que todos sus lados y ángulos son iguales, entonces el ángulo central será igual para cada uno de sus lados.
4. Paso 4: Si el polígono es irregular, cada uno de los lados puede tener un ángulo central diferente. En este caso, necesitarás calcular individualmente el ángulo central para cada lado sumando o restando grados según la configuración específica del polígono.
5. Paso 5: Utiliza la medida del ángulo central para resolver problemas o determinar propiedades adicionales del polígono. Por ejemplo, puedes calcular el ángulo central de un pentágono regular para saber qué tan "abierto" está y si se parece más a una estrella o a un hexágono regular.

Ahora que conoces estos cinco pasos infalibles, podrás desbloquear el misterio del ángulo central de cualquier polígono. Ya sea que estés resolviendo problemas matemáticos en el aula o explorando la geometría por pura diversión, esta información te permitirá comprender mejor las propiedades y características fundamentales de los polígonos. ¡No esperes más y adéntrate en el fascinante mundo de la geometría!

Cuál es la fórmula para calcular el ángulo central de un polígono regular

Calcular el ángulo central de un polígono regular puede parecer todo un misterio para muchos. Sin embargo, con estos cinco sencillos pasos podrás desbloquear el secreto y descubrir cómo obtener este valor tan importante en la geometría.

Paso 1: Conoce la definición del ángulo central

Antes de comenzar a calcular, es fundamental entender qué es exactamente un ángulo central en un polígono regular. Un ángulo central se define como aquel que tiene su vértice en el centro del polígono y sus lados conectan el centro con dos puntos distintos del perímetro del mismo.

Paso 2: Identifica el número de lados del polígono

Para calcular el ángulo central, es necesario saber cuántos lados tiene el polígono. Para ello, simplemente cuenta el número de segmentos que forman las caras del polígono. Si, por ejemplo, estamos trabajando con un hexágono regular, tendremos seis lados.

Paso 3: Utiliza la fórmula del ángulo central

Fórmula: Ángulo Central = 360° / n

Ahora que conoces la cantidad de lados del polígono (n), puedes aplicar la fórmula del ángulo central. Simplemente divide 360 grados entre el número de lados del polígono y obtendrás el valor buscado. Siguiendo el ejemplo anterior, para un hexágono regular, la fórmula quedaría así:

Ángulo Central = 360° / 6 = 60°

Paso 4: Realiza el cálculo

Para obtener el ángulo central del polígono, simplemente realiza la operación indicada en la fórmula. En nuestro ejemplo, realizamos la división 360° / 6 y obtuvimos un valor de 60°.

Paso 5: Verifica tus resultados

Finalmente, verifica tus resultados calculando nuevamente el ángulo central utilizando diferentes métodos o fórmulas alternativas para corroborar que obtienes el mismo valor. Esto te dará mayor confianza en tus cálculos y asegurará que tu respuesta es correcta.

Ahora que has desbloqueado el misterio, puedes calcular fácilmente el ángulo central de cualquier polígono regular siguiendo estos cinco pasos infalibles. Recuerda que la fórmula principal es Ángulo Central = 360° / n, donde n es el número de lados del polígono. ¡Así que ponte manos a la obra y deja de temer a los ángulos centrales!

Cómo puedo determinar el ángulo central de un polígono irregular

El ángulo central de un polígono irregular es una medida crucial que nos permite comprender mejor su estructura y propiedades geométricas. Al determinar el ángulo central, podemos desbloquear el misterio detrás de la forma y el comportamiento de un polígono específico. En este artículo, te guiaré a través de cinco pasos infalibles para calcular con precisión el ángulo central de cualquier polígono irregular.

Paso 1: Identifica el número de lados del polígono

Antes de determinar el ángulo central de un polígono, debemos conocer el número de lados que lo componen. Esto nos proporcionará una base sólida para el cálculo posterior. Observa cuidadosamente el polígono y cuenta el número de segmentos de línea que lo conforman. Pueden ser tantos como tres o más, dependiendo de la forma del polígono.

Paso 2: Encuentra el valor del ángulo interno

Para calcular el ángulo central, primero debemos encontrar el valor del ángulo interno del polígono. El ángulo interno es aquel formado por dos lados adyacentes dentro del polígono. Para hacer esto, utiliza la fórmula:

Ángulo interno = (n - 2) * 180 / n

Donde "n" es el número de lados del polígono identificado en el paso anterior. Aplica esta fórmula para encontrar el valor del ángulo interno. Toma nota del resultado obtenido, ya que lo necesitaremos para el cálculo posterior del ángulo central.

Paso 3: Identifica el vértice central

El vértice central es un punto dentro del polígono desde el cual podemos trazar líneas hacia los vértices exteriores. Este punto juega un papel clave en el cálculo del ángulo central. Observa la estructura del polígono y encuentra el vértice que creas que se encuentra en el centro del mismo. Recuerda, este puede estar ubicado en cualquier lugar dentro del polígono y puede no coincidir con ningún punto de intersección de las líneas que lo conforman.

Paso 4: Encuentra el ángulo central

Para determinar el ángulo central, debemos medir el ángulo formado entre dos líneas que conectan el vértice central con dos vértices externos del polígono. Utiliza una herramienta de medición adecuada, como un transportador, para encontrar con precisión el valor del ángulo central. Realiza varias mediciones para garantizar la exactitud de tu resultado. Registra el valor obtenido para su uso futuro.

Paso 5: Verificación

Finalmente, para asegurarnos de que hemos calculado correctamente el ángulo central, podemos realizar una verificación utilizando el valor del ángulo interno del polígono. Si multiplicamos el ángulo central por el número de lados del polígono, deberíamos obtener el valor del ángulo interno. Verifica que los resultados se correspondan y confirma que has desbloqueado exitosamente el misterio del ángulo central del polígono irregular.

Determinar el ángulo central de un polígono irregular puede parecer un desafío al principio, pero siguiendo estos cinco pasos infalibles podrás realizar el cálculo con precisión. Recuerda identificar el número de lados, encontrar el valor del ángulo interno, ubicar el vértice central, medir el ángulo central y verificar tus resultados. ¡Desbloquea el misterio del ángulo central y profundiza tu comprensión de los polígonos irregulares hoy mismo!

Cuáles son los pasos para encontrar el ángulo central de un polígono

El ángulo central de un polígono es un concepto fundamental en geometría. Este ángulo se define como aquel que se forma en el centro del polígono y tiene sus vértices en dos lados adyacentes. Su medida es esencial para comprender la estructura y las propiedades de los polígonos.

Aunque puede parecer complicado calcular el ángulo central de un polígono, en realidad es un proceso bastante sencillo. En este artículo, te mostraremos cinco pasos infalibles para desbloquear el misterio del ángulo central y facilitar su cálculo.

Paso 1: Identificar el número de lados del polígono

El primer paso para encontrar el ángulo central de un polígono es identificar cuántos lados tiene. Esto es crucial, ya que la fórmula para calcular el ángulo central varía según el número de lados del polígono. Puedes contar visualmente los lados del polígono o consultar la definición del mismo.

Paso 2: Aplicar la fórmula adecuada para el cálculo del ángulo central

Una vez que hayas determinado el número de lados del polígono, puedes aplicar la fórmula correspondiente para el cálculo del ángulo central. Aquí tienes algunas fórmulas comunes:

• Para un polígono regular, la fórmula es Ángulo Central = 360 grados / número de lados del polígono.
• Para un polígono irregular, la fórmula es Ángulo Central = 360 grados / suma de los ángulos exteriores del polígono.

Recuerda que el ángulo central se mide en grados, por lo que el resultado será también un valor en grados.

Paso 3: Reemplazar los valores en la fórmula y realizar los cálculos

Una vez que tengas la fórmula adecuada para el cálculo del ángulo central de tu polígono, puedes proceder a reemplazar los valores conocidos y realizar los cálculos. Asegúrate de utilizar la notación adecuada dependiendo del software o calculadora que estés utilizando.

Paso 4: Verificar tus resultados

Como en cualquier cálculo matemático, es importante verificar tus resultados para asegurarte de que sean precisos. Puedes hacerlo aplicando otras técnicas de medición angular o utilizando fuentes confiables para comparar tus resultados.

Paso 5: Utilizar el ángulo central en tus cálculos y análisis geométricos

Una vez que hayas encontrado el ángulo central de tu polígono, puedes utilizar este valor en diversos cálculos y análisis geométricos. El ángulo central es una medida clave para comprender las propiedades angulares de los polígonos y puede ser útil en diversas aplicaciones prácticas, como la construcción, la ingeniería y la programación de gráficos por computadora.

Desbloquear el misterio del ángulo central de un polígono no es tan complicado como puede parecer. Siguiendo estos cinco pasos infalibles, podrás encontrar fácilmente la medida del ángulo central y utilizarla en tus cálculos geométricos. Así que ¡adelante, desafía al misterio y adéntrate en el fascinante mundo de los polígonos!

Qué herramientas puedo usar para medir el ángulo central de un polígono en la vida real

Medir el ángulo central de un polígono en la vida real puede resultar complicado si no se utilizan las herramientas adecuadas. Afortunadamente, existen varios instrumentos que pueden ayudarte a desbloquear este misterio geométrico sin dificultad. A continuación te presentamos cinco herramientas infalibles para medir el ángulo central de un polígono:

1. Transportador

El transporte es una herramienta clásica y confiable para medir ángulos en cualquier tipo de polígono. Puedes encontrar transportadores de plástico o metal en diversas tiendas de suministros escolares o tiendas especializadas en herramientas de medición. Para utilizar el transportador, simplemente colócalo sobre el vértice del ángulo central y alinea uno de sus lados con uno de los lados del ángulo. Luego, lee el número que corresponde al ángulo central en la escala circular o semicircular del transportador.

2. Goniómetro

Si estás buscando una herramienta más precisa y profesional, el goniómetro es tu mejor opción. Este instrumento de medición angular se utiliza comúnmente en campos como la ingeniería y la arquitectura. Al igual que el transportador, el goniómetro se coloca sobre el vértice del ángulo central, pero utiliza una escala graduada con mayor precisión. Puedes encontrar goniómetros en tiendas especializadas en instrumentos de medición o en línea.

3. Software de diseño asistido por computadora (CAD)

Si eres más adepto a la tecnología, puedes utilizar software de diseño asistido por computadora (CAD) para medir el ángulo central de un polígono. Estos programas te permiten crear figuras geométricas precisas y realizar mediciones exactas de sus ángulos. Simplemente dibuja el polígono en el programa, identifica el ángulo central y el software te proporcionará su medida automáticamente.

4. Aplicaciones móviles

En la era digital, casi todo se puede hacer desde una aplicación móvil, ¡y medir ángulos centrales no es la excepción! Existen varias aplicaciones gratuitas disponibles tanto para iOS como para Android que te permiten medir ángulos utilizando la cámara de tu teléfono o mediante interacciones táctiles. Estas aplicaciones son muy útiles cuando necesitas medir ángulos rápidamente y no tienes acceso a herramientas físicas específicas.

5. Fórmulas matemáticas y cálculos

Si prefieres hacer tus propios cálculos, puedes utilizar fórmulas matemáticas específicas para determinar el ángulo central de un polígono. Para ello, necesitarás conocer la cantidad de lados del polígono y los datos necesarios para aplicar las fórmulas correspondientes. Esta opción es más recomendada para aquellos con conocimientos avanzados en matemáticas y que estén dispuestos a invertir tiempo en cálculos precisos.

Medir el ángulo central de un polígono en la vida real no tiene por qué ser complicado. Con las herramientas adecuadas, ya sea un transportador, un goniómetro, software de CAD, aplicaciones móviles o fórmulas matemáticas, podrás desbloquear este misterio geométrico con facilidad. ¡No dejes que el ángulo central te desconcierte y atrévete a explorar el fascinante mundo de la geometría!

Cuál es la importancia práctica de comprender el ángulo central de un polígono

Para comprender la importancia práctica de comprender el ángulo central de un polígono, es necesario entender primero qué es un ángulo central y cómo se relaciona con los polígonos. Un ángulo central es aquel que se forma en el centro de un círculo y cuya medida se toma entre dos radios que parten desde el centro hasta dos puntos del perímetro del círculo.

Pero, ¿qué tiene que ver esto con los polígonos? Los polígonos son figuras geométricas planas que están formadas por una serie de sides rectos y que tienen un número determinado de vértices. Al conocer el ángulo central de un polígono, podemos obtener información valiosa sobre las medidas y características de sus lados y ángulos internos.

Por ejemplo, si conocemos el ángulo central de un polígono regular, es decir, aquel que tiene todos sus lados y ángulos internos iguales, podremos determinar fácilmente la medida de cada uno de esos ángulos internos. Esta información puede ser de gran utilidad en diversas aplicaciones cotidianas.

Aplicación en construcción y arquitectura

En el campo de la construcción y arquitectura, comprender el ángulo central de un polígono puede ser fundamental para realizar diseños y cálculos precisos. Por ejemplo, al construir una estructura con forma de polígono regular, como un octógono, conocer el ángulo central nos permitirá determinar con exactitud la inclinación de las paredes y la ubicación de puertas y ventanas.

Además, al comprender cómo el ángulo central de un polígono afecta a los ángulos internos del mismo, también podemos determinar cómo distribuir la carga de manera uniforme en estructuras más complejas. Esto es especialmente relevante en puentes y edificios de gran escala donde la resistencia y estabilidad son fundamentales.

Aplicación en diseño gráfico y animación

Otra área donde el conocimiento del ángulo central de un polígono es fundamental es en el diseño gráfico y la animación. Al comprender cómo se comportan los ángulos internos de un polígono al variar el ángulo central, los diseñadores gráficos y animadores pueden crear formas y efectos visuales más dinámicos y realistas.

Por ejemplo, al utilizar software de diseño gráfico o animación, es común trabajar con polígonos para crear personajes o elementos gráficos. Si se comprende cómo afecta el ángulo central al comportamiento de esos polígonos, se puede lograr una mayor expresividad y movimiento en las creaciones.

Aplicación en geografía y cartografía

En geografía y cartografía, comprender el ángulo central de un polígono puede ser clave para proyectar mapas de manera adecuada. Los mapas utilizan proyecciones cartográficas para representar la superficie de la Tierra en un plano, y estas proyecciones pueden basarse en polígonos regulares o irregulares.

Al conocer el ángulo central de los polígonos utilizados en la proyección cartográfica, los expertos pueden crear mapas más precisos y evitar distorsiones significativas. Esto es especialmente importante al trabajar con mapas de gran escala, donde cada grado de diferencia puede marcar una gran variación en la representación.

Comprender el ángulo central de un polígono tiene múltiples aplicaciones prácticas en diversos campos como la construcción, arquitectura, diseño gráfico, animación, geografía y cartografía. Su conocimiento nos permite realizar cálculos precisos, diseñar estructuras estables, crear elementos visuales impactantes y proyectar mapas con exactitud. Por lo tanto, desbloquear el misterio del ángulo central de un polígono a través de estos cinco pasos infalibles es un paso clave para ampliar nuestro conocimiento y potenciar nuestras habilidades en estas áreas. ¡No esperes más y adéntrate en el fascinante mundo de los polígonos y sus ángulos centrales!

Cómo puedo aplicar el conocimiento del ángulo central en situaciones cotidianas

El ángulo central es un concepto matemático que se aplica en muchos aspectos de nuestra vida cotidiana, aunque a veces no nos demos cuenta. Comprender cómo funciona y poder desbloquear el misterio de este ángulo nos puede ayudar a resolver problemas e incluso tomar decisiones más informadas.

1. Identifica el ángulo central: Lo primero que debes hacer es identificar el ángulo central en la figura o situación en la que te encuentres. El ángulo central es aquel que se forma en el centro de un polígono cuando se trazan dos segmentos desde sus vértices hasta el centro.

2. Mide su amplitud: Una vez identificado el ángulo central, debes medir su amplitud. La amplitud de un ángulo se mide en grados y nos indica qué tanto se abre o cierra dicho ángulo. Puedes utilizar un transportador o una herramienta de medición para obtener con precisión el valor numérico de su amplitud.

3. Relaciona el ángulo central con los ángulos del polígono: El ángulo central está relacionado con los ángulos interiores del polígono en el que se encuentra. De hecho, la amplitud del ángulo central es igual a la suma de las amplitudes de los ángulos interiores del polígono. Esta relación nos permite inferir información sobre los demás ángulos a partir del ángulo central.

4. Aplica el ángulo central en la resolución de problemas: Una vez que has identificado y comprendido la relación del ángulo central con los demás ángulos del polígono, puedes utilizar este conocimiento para resolver problemas geométricos. Por ejemplo, si conoces el valor del ángulo central de un polígono regular, puedes determinar la amplitud de cada uno de sus ángulos interiores utilizando la fórmula adecuada.

5. Utiliza el ángulo central en decisiones cotidianas: Además de su aplicación en problemas matemáticos, el conocimiento del ángulo central también puede ser útil en situaciones cotidianas. Por ejemplo, si estás diseñando una habitación y quieres distribuir de manera equitativa los muebles alrededor de una mesa central, puedes utilizar el ángulo central para calcular la separación adecuada entre cada uno de ellos.

Desbloquear el misterio del ángulo central nos permite comprender mejor las propiedades y relaciones de los polígonos, y nos brinda herramientas para resolver problemas tanto en el ámbito matemático como en nuestro día a día. Aplica estos cinco pasos infalibles y descubre toda la utilidad que el ángulo central puede ofrecerte.

Existen ejemplos famosos en los que el ángulo central haya sido utilizado

El ángulo central de un polígono es un concepto fundamental en la geometría. Nos permite comprender el comportamiento y las relaciones entre los lados y los ángulos de un polígono. Aunque puede parecer complicado al principio, desbloquear el misterio del ángulo central es más sencillo de lo que crees.

1. Definición del ángulo central

Antes de sumergirnos en los ejemplos famosos en los que el ángulo central se ha utilizado, es importante comprender qué es exactamente un ángulo central. En pocas palabras, el ángulo central de un polígono es aquel que se forma al trazar dos radios desde su centro hacia dos puntos cualesquiera de su circunferencia.

Este ángulo central se mide en grados y puede variar en tamaño dependiendo del número de lados del polígono. Por ejemplo, un triángulo equilátero tendría un ángulo central de 120 grados, mientras que un hexágono regular tendría un ángulo central de 60 grados.

2. Ejemplo 1: La rueda de la fortuna

Un ejemplo famoso en el que se utiliza el ángulo central es en una rueda de la fortuna. Imagina que estás en un parque de diversiones y decides subir a una enorme rueda que gira lentamente. Si te detienes en un punto aleatorio de la circunferencia de la rueda y dibujas un segmento desde el centro hasta ese punto, habrás trazado un ángulo central.

Este ángulo central te permite comprender cuánto ha rotado el punto en relación con la posición inicial. Si giras 90 grados, estarías en un ángulo central de 90 grados. Si giras 180 grados, estarías en un ángulo central de 180 grados, es decir, has dado la vuelta completa a la circunferencia.

3. Ejemplo 2: El reloj

Otro ejemplo clásico en el que se aplica el concepto del ángulo central es en los relojes analógicos. Cada hora, el segundero, el minutero y el horario marcan diferentes ángulos centrales. Por ejemplo, cuando el minutero está apuntando al número 12 y el segundo está en el número 6, habrá un ángulo central de 180 grados entre ellos.

Observar el reloj es una excelente manera de visualizar y comprender cómo funcionan los ángulos centrales en la vida cotidiana.

4. Ejemplo 3: La ruleta

La ruleta es otro ejemplo famoso en el que el ángulo central juega un papel crucial. Imagina que estás en un casino y decides apostar tus fichas en un número específico. Cuando la bola de la ruleta se detiene en ese número y trazas un segmento desde el centro de la ruleta hasta ese número, estás creando un ángulo central.

En este escenario, el ángulo central le permite al crupier determinar si tu apuesta fue ganadora o no. Dependiendo del número y la posición de tu apuesta, el ángulo central te dirá si has tenido suerte o no en ese giro de la ruleta.

5. Ejemplo 4: Los diferentes polígonos

Un último ejemplo común donde se utiliza el ángulo central es al analizar las propiedades de diferentes polígonos. Rectángulos, cuadrados, hexágonos, octógonos y otros polígonos regulares tienen sus propios ángulos centrales característicos.

Entender los ángulos centrales de estos polígonos nos permite predecir y calcular con precisión otros elementos relacionados, como las medidas de los ángulos internos y externos, la longitud de los lados, las áreas y los perímetros.

El ángulo central de un polígono es un concepto clave para comprender cómo se comportan los polígonos en diferentes contextos. A través de ejemplos famosos, como la rueda de la fortuna, el reloj, la ruleta y los polígonos regulares, podemos visualizar mejor y desbloquear el misterio del ángulo central. ¡Así que no temas explorar y experimentar con los ángulos centrales en tu propio entorno!

Qué otras propiedades interesantes están relacionadas con el ángulo central de un polígono

El ángulo central de un polígono es uno de los conceptos más fascinantes en el estudio de la geometría. No solo nos permite comprender mejor la estructura y características de los polígonos, sino que también está estrechamente relacionado con otras propiedades igualmente interesantes.

1. Relación entre el ángulo central y el número de lados de un polígono

Una propiedad fundamental del ángulo central es su relación directa con el número de lados de un polígono. Si consideramos un polígono regular, aquel que tiene todos sus lados y ángulos iguales, podemos establecer una fórmula para calcular el valor del ángulo central. Basta con dividir 360 grados entre el número de lados del polígono para obtener el valor del ángulo central en grados. Por ejemplo, si tenemos un hexágono regular, sabemos que posee 6 lados, entonces el ángulo interior central será de 60 grados.

2. La suma de los ángulos centrales de un polígono completo

Otra propiedad intrigante del ángulo central es su relación con la suma total de los ángulos centrales de un polígono completo. La suma de los ángulos centrales de un polígono completo siempre será igual a 360 grados. Esto significa que sin importar la forma o el número de lados que tenga el polígono, si sumamos todos los ángulos centrales obtendremos como resultado siempre 360 grados. Es un hallazgo sorprendente que demuestra cómo la geometría está intrínsecamente equilibrada y organizada.

3. Relación entre el ángulo central y el ángulo interior de un polígono

Otra propiedad intrigante del ángulo central es su relación con el ángulo interior de un polígono regular. Si dividimos el ángulo central por 2, obtendremos el valor del ángulo interior correspondiente. Esto significa que el ángulo interior de un polígono regular siempre será la mitad del ángulo central. Por ejemplo, si consideramos un pentágono regular cuyo ángulo central es de 72 grados, sabemos que cada uno de sus ángulos interiores será de 36 grados.

4. Aplicaciones del ángulo central en la trigonometría

El ángulo central también juega un papel importante en la trigonometría. Al estudiar las funciones trigonométricas seno, coseno y tangente, podemos relacionarlas con el ángulo central de un polígono y obtener resultados significativos. Estas funciones nos permiten calcular longitudes de lados y medidas de ángulos en triángulos. A través de la relación entre el ángulo central y el ángulo interior de un polígono, podemos aplicar las funciones trigonométricas para resolver problemas geométricos más complejos y realizar cálculos precisos.

5. Relación entre el ángulo central y la simetría en los polígonos

La aparición del ángulo central también está estrechamente relacionada con la simetría en los polígonos. Cuando consideramos un polígono regular, todos sus ángulos centrales serán iguales. Esto implica que cada uno de los ángulos centrales está simétricamente distribuido alrededor del centro del polígono. Esta propiedad de simetría marca la estructura y forma del polígono, otorgándole una estética balanceada y atractiva.

El ángulo central de un polígono se encuentra en el núcleo de numerosas propiedades geométricas fascinantes. Su relación con el número de lados, la suma total de los ángulos centrales, el ángulo interior, las aplicaciones trigonométricas y la simetría en los polígonos amplían nuestra comprensión del mundo de la geometría. Desbloquear el misterio del ángulo central es descubrir un tesoro oculto que nos permite explorar las intrincadas conexiones de la geometría y su relevancia en nuestras vidas cotidianas.

Preguntas frecuentes (FAQ)

1. ¿Qué es un ángulo central en un polígono?

Es el ángulo formado por dos radios contiguos que parten desde el centro del polígono hacia dos vértices consecutivos.

2. ¿Cuánto mide un ángulo central en un polígono regular?

En un polígono regular, todos los ángulos centrales tienen la misma medida y esta se calcula dividiendo 360 grados entre el número de lados del polígono.

3. ¿Cuál es la relación entre un ángulo central y un ángulo inscrito en un polígono?

La medida de un ángulo central es el doble de la medida de su correspondiente ángulo inscrito en el mismo arco.

4. ¿Cuál es la suma de los ángulos centrales de un polígono?

La suma de los ángulos centrales de un polígono se calcula multiplicando el número de lados del polígono por 180 grados.

5. ¿Cómo se calcula la medida de un ángulo central si conocemos la medida de un ángulo inscrito?

Para calcular la medida del ángulo central a partir del ángulo inscrito, simplemente se multiplica la medida del ángulo inscrito por 2.